Question Number 133923 by bemath last updated on 25/Feb/21
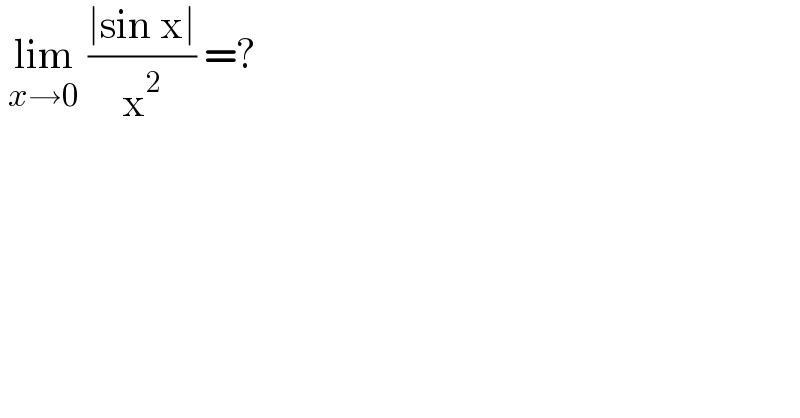
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mid\mathrm{sin}\:\mathrm{x}\mid}{\mathrm{x}^{\mathrm{2}} }\:=? \\ $$
Answered by EDWIN88 last updated on 25/Feb/21
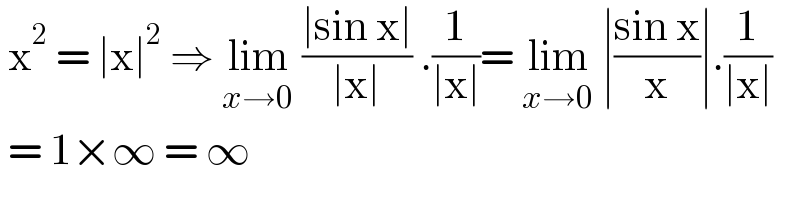
$$\:\mathrm{x}^{\mathrm{2}} \:=\:\mid\mathrm{x}\mid^{\mathrm{2}} \:\Rightarrow\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mid\mathrm{sin}\:\mathrm{x}\mid}{\mid\mathrm{x}\mid}\:.\frac{\mathrm{1}}{\mid\mathrm{x}\mid}=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mid\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{x}}\mid.\frac{\mathrm{1}}{\mid\mathrm{x}\mid} \\ $$$$\:=\:\mathrm{1}×\infty\:=\:\infty\: \\ $$
