Question Number 142307 by qaz last updated on 29/May/21
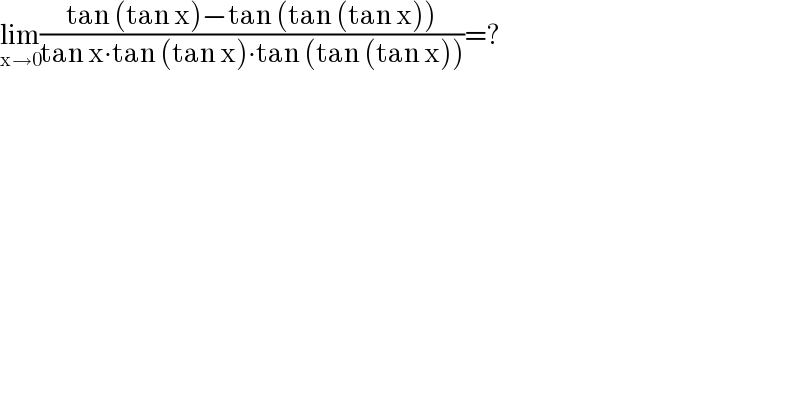
$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{tan}\:\left(\mathrm{tan}\:\mathrm{x}\right)−\mathrm{tan}\:\left(\mathrm{tan}\:\left(\mathrm{tan}\:\mathrm{x}\right)\right)}{\mathrm{tan}\:\mathrm{x}\centerdot\mathrm{tan}\:\left(\mathrm{tan}\:\mathrm{x}\right)\centerdot\mathrm{tan}\:\left(\mathrm{tan}\:\left(\mathrm{tan}\:\mathrm{x}\right)\right)}=? \\ $$
Answered by Dwaipayan Shikari last updated on 29/May/21
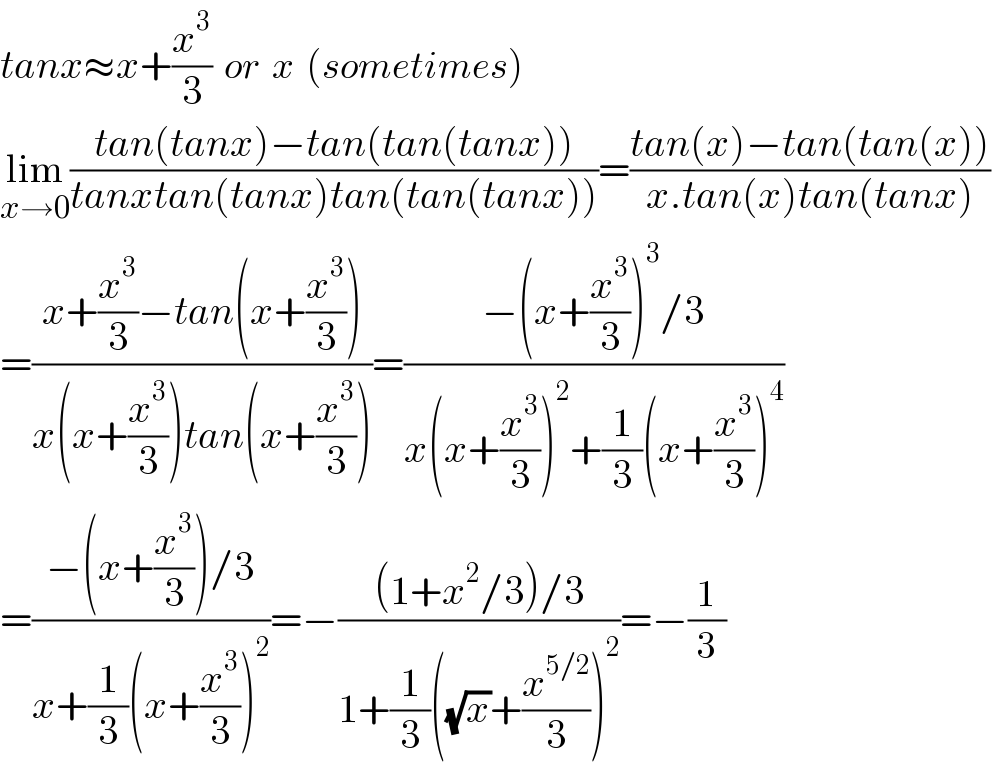
$${tanx}\approx{x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\:\:{or}\:\:{x}\:\:\left({sometimes}\right) \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{tan}\left({tanx}\right)−{tan}\left({tan}\left({tanx}\right)\right)}{{tanxtan}\left({tanx}\right){tan}\left({tan}\left({tanx}\right)\right)}=\frac{{tan}\left({x}\right)−{tan}\left({tan}\left({x}\right)\right)}{{x}.{tan}\left({x}\right){tan}\left({tanx}\right)} \\ $$$$=\frac{{x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}−{tan}\left({x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\right)}{{x}\left({x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\right){tan}\left({x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\right)}=\frac{−\left({x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\right)^{\mathrm{3}} /\mathrm{3}}{{x}\left({x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{3}}\left({x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\right)^{\mathrm{4}} } \\ $$$$=\frac{−\left({x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\right)/\mathrm{3}}{{x}+\frac{\mathrm{1}}{\mathrm{3}}\left({x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\right)^{\mathrm{2}} }=−\frac{\left(\mathrm{1}+{x}^{\mathrm{2}} /\mathrm{3}\right)/\mathrm{3}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}\left(\sqrt{{x}}+\frac{{x}^{\mathrm{5}/\mathrm{2}} }{\mathrm{3}}\right)^{\mathrm{2}} }=−\frac{\mathrm{1}}{\mathrm{3}} \\ $$
