Question Number 142171 by iloveisrael last updated on 27/May/21
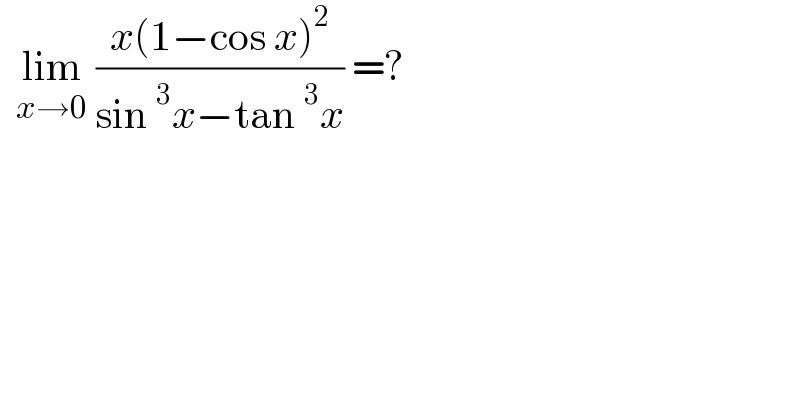
$$\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}\left(\mathrm{1}−\mathrm{cos}\:{x}\right)^{\mathrm{2}} }{\mathrm{sin}\:^{\mathrm{3}} {x}−\mathrm{tan}\:^{\mathrm{3}} {x}}\:=? \\ $$
Answered by iloveisrael last updated on 27/May/21
![lim_(x→0) ((x(2sin^2 ((x/2)))^2 )/(tan^3 x(cos^3 x−1))) = lim_(x→0) ((4sin^4 ((x/2)))/(tan^2 x(−2sin^2 ((x/2)))(cos^2 x+cos x+1))) = (1/3).lim_(x→0) ((−2sin^2 ((x/2)))/(tan^2 x)) = (1/3). [−2((1/4))] = −(1/6).](https://www.tinkutara.com/question/Q142177.png)
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}\left(\mathrm{2sin}\:^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\right)^{\mathrm{2}} }{\mathrm{tan}\:^{\mathrm{3}} {x}\left(\mathrm{cos}\:^{\mathrm{3}} {x}−\mathrm{1}\right)}\:= \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{4sin}\:^{\mathrm{4}} \left(\frac{{x}}{\mathrm{2}}\right)}{\mathrm{tan}\:^{\mathrm{2}} {x}\left(−\mathrm{2sin}\:^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\right)\left(\mathrm{cos}\:^{\mathrm{2}} {x}+\mathrm{cos}\:{x}+\mathrm{1}\right)}\:= \\ $$$$\:\:\frac{\mathrm{1}}{\mathrm{3}}.\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{2sin}\:^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}{\mathrm{tan}\:^{\mathrm{2}} {x}}\:=\:\frac{\mathrm{1}}{\mathrm{3}}.\:\left[−\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\right] \\ $$$$\:=\:−\frac{\mathrm{1}}{\mathrm{6}}.\: \\ $$
Answered by liberty last updated on 27/May/21
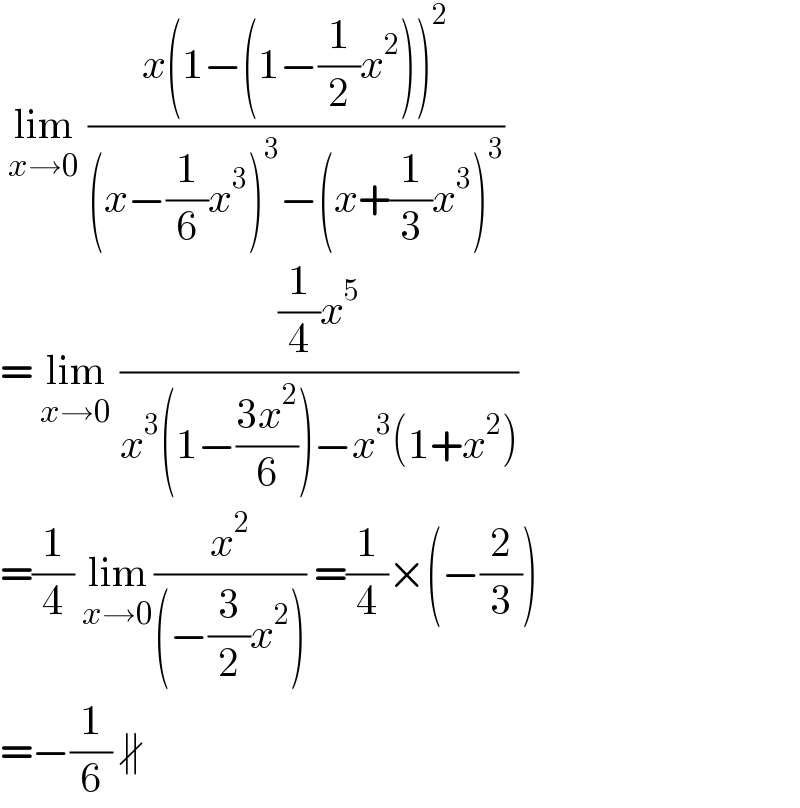
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}\left(\mathrm{1}−\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} \right)\right)^{\mathrm{2}} }{\left({x}−\frac{\mathrm{1}}{\mathrm{6}}{x}^{\mathrm{3}} \right)^{\mathrm{3}} −\left({x}+\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{3}} \right)^{\mathrm{3}} } \\ $$$$=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{\mathrm{1}}{\mathrm{4}}{x}^{\mathrm{5}} }{{x}^{\mathrm{3}} \left(\mathrm{1}−\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{6}}\right)−{x}^{\mathrm{3}} \left(\mathrm{1}+{x}^{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}^{\mathrm{2}} }{\left(−\frac{\mathrm{3}}{\mathrm{2}}{x}^{\mathrm{2}} \right)}\:=\frac{\mathrm{1}}{\mathrm{4}}×\left(−\frac{\mathrm{2}}{\mathrm{3}}\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{6}}\:\nparallel \\ $$
Answered by som(math1967) last updated on 27/May/21

$$\underset{\boldsymbol{{x}}\rightarrow\mathrm{0}} {\boldsymbol{{lim}}}\frac{\boldsymbol{{x}}\left(\mathrm{1}−\boldsymbol{{cosx}}\right)^{\mathrm{2}} }{\boldsymbol{{sin}}^{\mathrm{3}} \boldsymbol{{x}}\left(\mathrm{1}−\frac{\mathrm{1}}{\boldsymbol{{cos}}^{\mathrm{3}} \boldsymbol{{x}}}\right)} \\ $$$$\underset{\boldsymbol{{x}}\rightarrow\mathrm{0}} {\boldsymbol{{lim}}}\:\frac{\mathrm{1}}{\frac{{sinx}}{\boldsymbol{{x}}}}×\frac{\left(\mathrm{1}−\boldsymbol{{cosx}}\right)^{\mathrm{2}} }{\boldsymbol{{sin}}^{\mathrm{2}} \boldsymbol{{x}}\left(\boldsymbol{{cos}}^{\mathrm{3}} \boldsymbol{{x}}−\mathrm{1}\right)}×\boldsymbol{{cos}}^{\mathrm{3}} \boldsymbol{{x}} \\ $$$$\underset{\boldsymbol{{x}}\rightarrow\mathrm{0}} {\boldsymbol{{lim}}}\:\frac{\left(\mathrm{1}−\boldsymbol{{cosx}}\right)^{\mathrm{2}} \boldsymbol{{cos}}^{\mathrm{3}} \boldsymbol{{x}}}{\left(\mathrm{1}−\boldsymbol{{cosx}}\right)\left(\mathrm{1}+\boldsymbol{{cosx}}\right)\left(\boldsymbol{{cosx}}−\mathrm{1}\right)\left(\boldsymbol{{cos}}^{\mathrm{2}} \boldsymbol{{x}}+\boldsymbol{{cosx}}+\mathrm{1}\right)} \\ $$$$\underset{\boldsymbol{{x}}\rightarrow\mathrm{0}} {\boldsymbol{{lim}}}\:\frac{−\boldsymbol{{cos}}^{\mathrm{3}} \boldsymbol{{x}}}{\left(\mathrm{1}+\boldsymbol{{cosx}}\right)\left(\boldsymbol{{cos}}^{\mathrm{2}} \boldsymbol{{x}}+\boldsymbol{{cosx}}+\mathrm{1}\right)}=\frac{−\mathrm{1}}{\left(\mathrm{1}+\mathrm{1}\right)\left(\mathrm{1}+\mathrm{1}+\mathrm{1}\right)} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{6}} \\ $$
