Question Number 141965 by gsk2684 last updated on 25/May/21
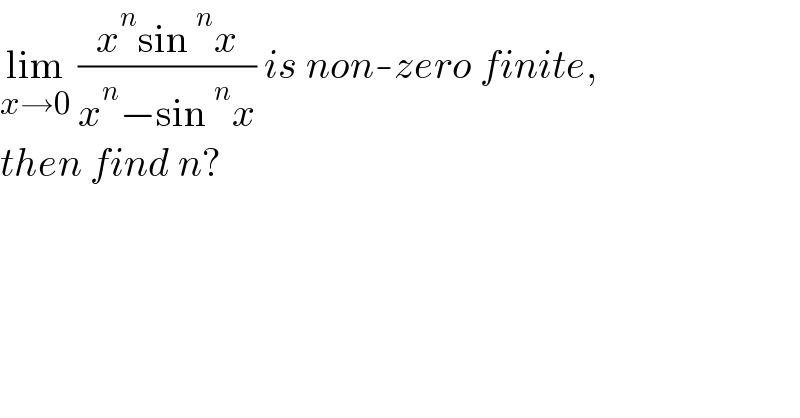
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}^{{n}} \mathrm{sin}\:^{{n}} {x}}{{x}^{{n}} −\mathrm{sin}\:^{{n}} {x}}\:{is}\:{non}-{zero}\:{finite},\: \\ $$$${then}\:{find}\:{n}? \\ $$
Commented by gsk2684 last updated on 25/May/21

$${solution}\:{please} \\ $$
Answered by Dwaipayan Shikari last updated on 25/May/21
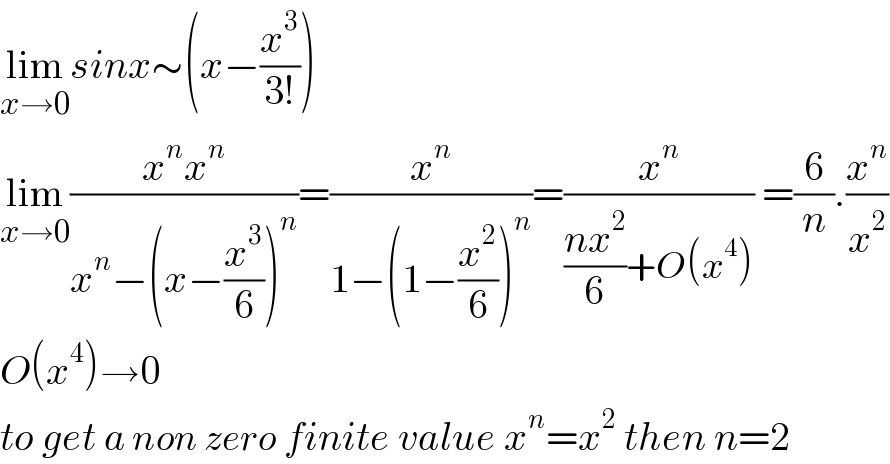
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{sinx}\sim\left({x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}\right) \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}^{{n}} {x}^{{n}} }{{x}^{{n}} −\left({x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\right)^{{n}} }=\frac{{x}^{{n}} }{\mathrm{1}−\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{6}}\right)^{{n}} }=\frac{{x}^{{n}} }{\frac{{nx}^{\mathrm{2}} }{\mathrm{6}}+{O}\left({x}^{\mathrm{4}} \right)}\:=\frac{\mathrm{6}}{{n}}.\frac{{x}^{{n}} }{{x}^{\mathrm{2}} } \\ $$$${O}\left({x}^{\mathrm{4}} \right)\rightarrow\mathrm{0} \\ $$$${to}\:{get}\:{a}\:{non}\:{zero}\:{finite}\:{value}\:{x}^{{n}} ={x}^{\mathrm{2}} \:{then}\:{n}=\mathrm{2} \\ $$
Commented by gsk2684 last updated on 25/May/21

$${thank}\:{you} \\ $$
