Question Number 131962 by EDWIN88 last updated on 10/Feb/21
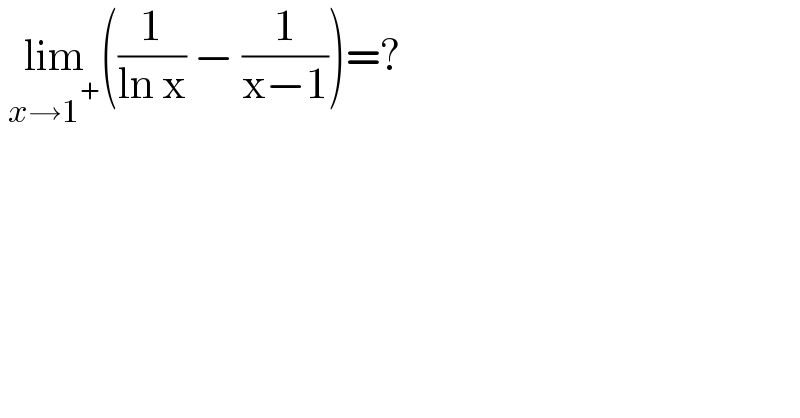
$$\:\underset{{x}\rightarrow\mathrm{1}^{+} } {\mathrm{lim}}\left(\frac{\mathrm{1}}{\mathrm{ln}\:\mathrm{x}}\:−\:\frac{\mathrm{1}}{\mathrm{x}−\mathrm{1}}\right)=? \\ $$
Answered by liberty last updated on 10/Feb/21
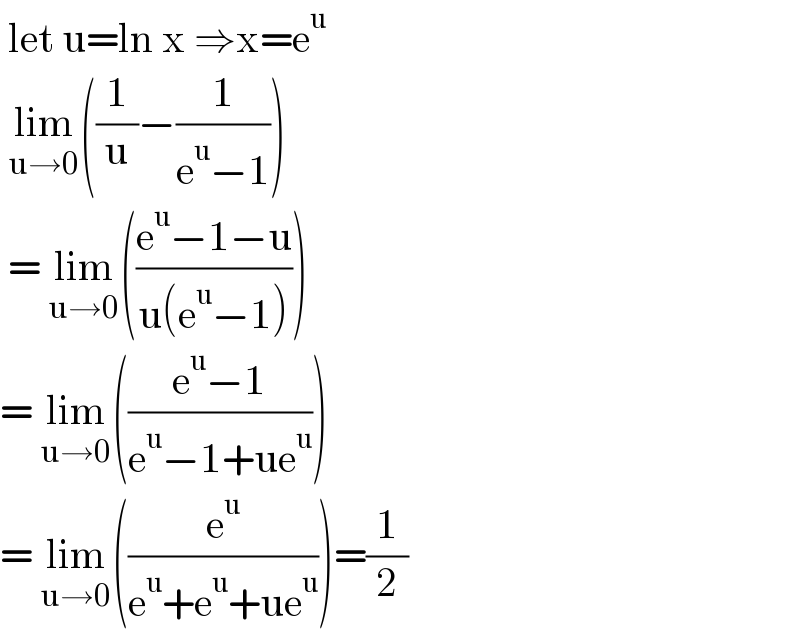
$$\:\mathrm{let}\:\mathrm{u}=\mathrm{ln}\:\mathrm{x}\:\Rightarrow\mathrm{x}=\mathrm{e}^{\mathrm{u}} \\ $$$$\:\underset{\mathrm{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}}{\mathrm{u}}−\frac{\mathrm{1}}{\mathrm{e}^{\mathrm{u}} −\mathrm{1}}\right) \\ $$$$\:=\:\underset{\mathrm{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{e}^{\mathrm{u}} −\mathrm{1}−\mathrm{u}}{\mathrm{u}\left(\mathrm{e}^{\mathrm{u}} −\mathrm{1}\right)}\right) \\ $$$$=\:\underset{\mathrm{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{e}^{\mathrm{u}} −\mathrm{1}}{\mathrm{e}^{\mathrm{u}} −\mathrm{1}+\mathrm{ue}^{\mathrm{u}} }\right) \\ $$$$=\:\underset{\mathrm{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{e}^{\mathrm{u}} }{\mathrm{e}^{\mathrm{u}} +\mathrm{e}^{\mathrm{u}} +\mathrm{ue}^{\mathrm{u}} }\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
