lim-x-1-2-x-x-

Question Number 66019 by Rio Michael last updated on 07/Aug/19

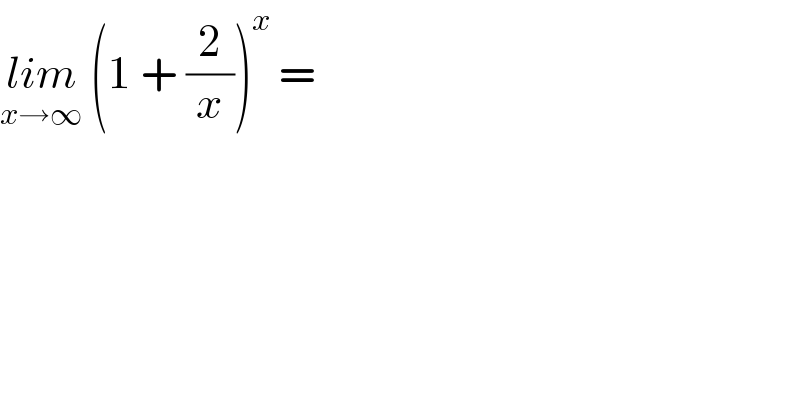
$$\underset{{x}\rightarrow\infty} {{lim}}\:\left(\mathrm{1}\:+\:\frac{\mathrm{2}}{{x}}\right)^{{x}} \:= \\ $$

Commented by mathmax by abdo last updated on 07/Aug/19

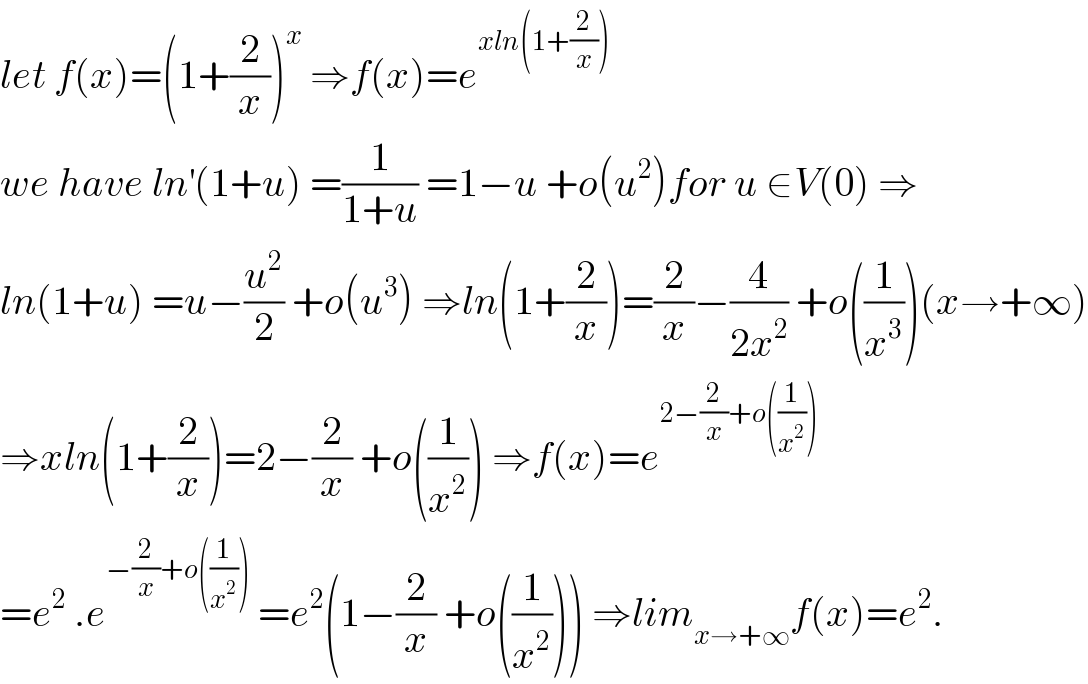
let f(x)=(1+(2/x))^x ⇒f(x)=e^(xln(1+(2/x))) we have ln^′ (1+u) =(1/(1+u)) =1−u +o(u^2 )for u ∈V(0) ⇒ ln(1+u) =u−(u^2 /2) +o(u^3 ) ⇒ln(1+(2/x))=(2/x)−(4/(2x^2 )) +o((1/x^3 ))(x→+∞) ⇒xln(1+(2/x))=2−(2/x) +o((1/x^2 )) ⇒f(x)=e^(2−(2/x)+o((1/x^2 ))) =e^2 .e^(−(2/x)+o((1/x^2 ))) =e^2 (1−(2/x) +o((1/x^2 ))) ⇒lim_(x→+∞) f(x)=e^2 .

$${let}\:{f}\left({x}\right)=\left(\mathrm{1}+\frac{\mathrm{2}}{{x}}\right)^{{x}} \:\Rightarrow{f}\left({x}\right)={e}^{{xln}\left(\mathrm{1}+\frac{\mathrm{2}}{{x}}\right)} \\ $$$${we}\:{have}\:{ln}^{'} \left(\mathrm{1}+{u}\right)\:=\frac{\mathrm{1}}{\mathrm{1}+{u}}\:=\mathrm{1}−{u}\:+{o}\left({u}^{\mathrm{2}} \right){for}\:{u}\:\in{V}\left(\mathrm{0}\right)\:\Rightarrow \\ $$$${ln}\left(\mathrm{1}+{u}\right)\:={u}−\frac{{u}^{\mathrm{2}} }{\mathrm{2}}\:+{o}\left({u}^{\mathrm{3}} \right)\:\Rightarrow{ln}\left(\mathrm{1}+\frac{\mathrm{2}}{{x}}\right)=\frac{\mathrm{2}}{{x}}−\frac{\mathrm{4}}{\mathrm{2}{x}^{\mathrm{2}} }\:+{o}\left(\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\right)\left({x}\rightarrow+\infty\right) \\ $$$$\Rightarrow{xln}\left(\mathrm{1}+\frac{\mathrm{2}}{{x}}\right)=\mathrm{2}−\frac{\mathrm{2}}{{x}}\:+{o}\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)\:\Rightarrow{f}\left({x}\right)={e}^{\mathrm{2}−\frac{\mathrm{2}}{{x}}+{o}\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)} \\ $$$$={e}^{\mathrm{2}} \:.{e}^{−\frac{\mathrm{2}}{{x}}+{o}\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)} \:={e}^{\mathrm{2}} \left(\mathrm{1}−\frac{\mathrm{2}}{{x}}\:+{o}\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)\right)\:\Rightarrow{lim}_{{x}\rightarrow+\infty} {f}\left({x}\right)={e}^{\mathrm{2}} . \\ $$

Answered by Tanmay chaudhury last updated on 07/Aug/19

t=lim_(x→∞) (1+(2/x))^x y=(1/x) as x→∞ y→0 t=lim_(y→0) (1+2y)^(1/y) lnt=lim_(y→0) ((ln(1+2y))/(2y))×2 lnt=1×2 [formula lim_(x→0) ((ln(1+x))/x)=1] t=e^2 answer

$${t}=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{2}}{{x}}\right)^{{x}} \\ $$$${y}=\frac{\mathrm{1}}{{x}}\:\:\:{as}\:{x}\rightarrow\infty\:\:\:{y}\rightarrow\mathrm{0} \\ $$$${t}=\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\mathrm{1}+\mathrm{2}{y}\right)^{\frac{\mathrm{1}}{{y}}} \\ $$$${lnt}=\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{ln}\left(\mathrm{1}+\mathrm{2}{y}\right)}{\mathrm{2}{y}}×\mathrm{2} \\ $$$${lnt}=\mathrm{1}×\mathrm{2}\:\:\:\left[{formula}\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{ln}\left(\mathrm{1}+{x}\right)}{{x}}=\mathrm{1}\right] \\ $$$${t}={e}^{\mathrm{2}} \:\:{answer} \\ $$

Answered by kaivan.ahmadi last updated on 07/Aug/19

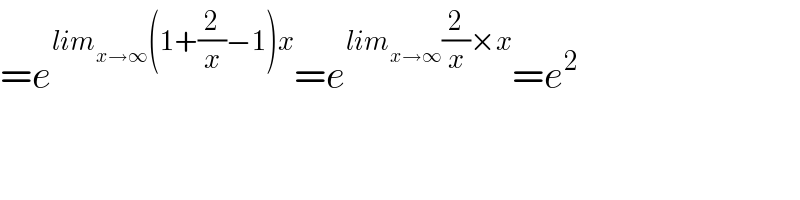
=e^(lim_(x→∞) (1+(2/x)−1)x) =e^(lim_(x→∞) (2/x)×x) =e^2

$$={e}^{{lim}_{{x}\rightarrow\infty} \left(\mathrm{1}+\frac{\mathrm{2}}{{x}}−\mathrm{1}\right){x}} ={e}^{{lim}_{{x}\rightarrow\infty} \frac{\mathrm{2}}{{x}}×{x}} ={e}^{\mathrm{2}} \\ $$

Commented by Rio Michael last updated on 07/Aug/19

please guys check my solution as i understand it. lim_(x→∞) (1 +(2/x))^x let (2/x) = (1/m) ⇒ x =2m such that x →∞ , m →∞ lim_(m→∞) [(1 + (1/m))^m ]^2 = e^2

$${please}\:{guys}\:{check}\:{my}\:{solution}\:{as}\:{i}\:{understand}\:{it}. \\ $$$$\:\underset{{x}\rightarrow\infty} {{lim}}\:\left(\mathrm{1}\:+\frac{\mathrm{2}}{{x}}\right)^{{x}} \\ $$$${let}\:\:\frac{\mathrm{2}}{{x}}\:=\:\frac{\mathrm{1}}{{m}} \\ $$$$\Rightarrow\:{x}\:=\mathrm{2}{m} \\ $$$${such}\:{that}\:\:{x}\:\rightarrow\infty\:,\:{m}\:\rightarrow\infty \\ $$$$\underset{{m}\rightarrow\infty} {{lim}}\left[\left(\mathrm{1}\:+\:\frac{\mathrm{1}}{{m}}\right)^{{m}} \right]^{\mathrm{2}} \\ $$$$\:=\:{e}^{\mathrm{2}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply