lim-x-1-lnx-ln-1-x-

Question Number 78122 by Tony Lin last updated on 14/Jan/20

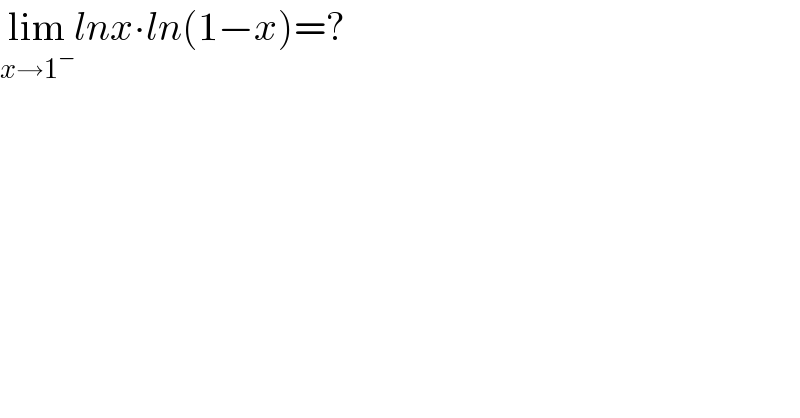
$$\underset{{x}\rightarrow\mathrm{1}^{−} } {\mathrm{lim}}{lnx}\centerdot{ln}\left(\mathrm{1}−{x}\right)=? \\ $$

Commented by msup trace by abdo last updated on 14/Jan/20

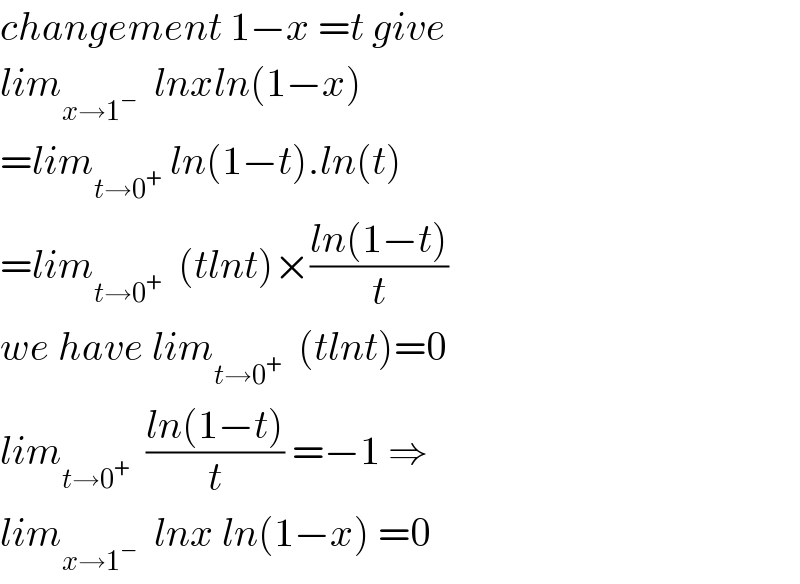
changement 1−x =t give lim_(x→1^− ) lnxln(1−x) =lim_(t→0^+ ) ln(1−t).ln(t) =lim_(t→0^+ ) (tlnt)×((ln(1−t))/t) we have lim_(t→0^+ ) (tlnt)=0 lim_(t→0^+ ) ((ln(1−t))/t) =−1 ⇒ lim_(x→1^− ) lnx ln(1−x) =0

$${changement}\:\mathrm{1}−{x}\:={t}\:{give} \\ $$$${lim}_{{x}\rightarrow\mathrm{1}^{−} } \:\:{lnxln}\left(\mathrm{1}−{x}\right) \\ $$$$={lim}_{{t}\rightarrow\mathrm{0}^{+} } \:{ln}\left(\mathrm{1}−{t}\right).{ln}\left({t}\right) \\ $$$$={lim}_{{t}\rightarrow\mathrm{0}^{+} } \:\:\left({tlnt}\right)×\frac{{ln}\left(\mathrm{1}−{t}\right)}{{t}} \\ $$$${we}\:{have}\:{lim}_{{t}\rightarrow\mathrm{0}^{+} } \:\:\left({tlnt}\right)=\mathrm{0} \\ $$$${lim}_{{t}\rightarrow\mathrm{0}^{+} } \:\:\frac{{ln}\left(\mathrm{1}−{t}\right)}{{t}}\:=−\mathrm{1}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{1}^{−} } \:\:{lnx}\:{ln}\left(\mathrm{1}−{x}\right)\:=\mathrm{0} \\ $$

Commented by Tony Lin last updated on 14/Jan/20