lim-x-1-x-1-ln-x-2-x-

Question Number 143462 by Willson last updated on 14/Jun/21

$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\:\:\frac{{x}−\mathrm{1}}{{ln}\left(\frac{{x}}{\mathrm{2}−{x}}\right)}\:=\:??? \\ $$

Answered by Dwaipayan Shikari last updated on 14/Jun/21

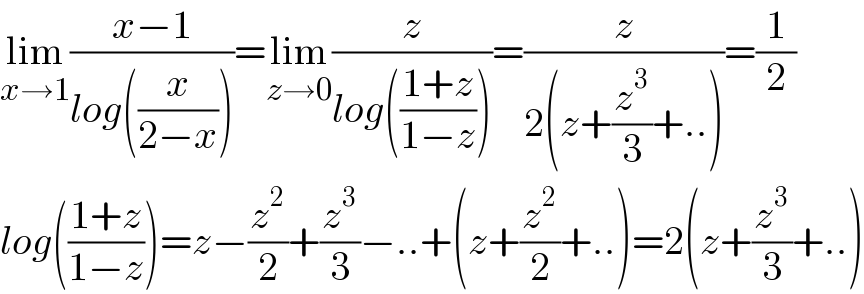
lim_(x→1) ((x−1)/(log((x/(2−x)))))=lim_(z→0) (z/(log(((1+z)/(1−z)))))=(z/(2(z+(z^3 /3)+..)))=(1/2) log(((1+z)/(1−z)))=z−(z^2 /2)+(z^3 /3)−..+(z+(z^2 /2)+..)=2(z+(z^3 /3)+..)

$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{{x}−\mathrm{1}}{{log}\left(\frac{{x}}{\mathrm{2}−{x}}\right)}=\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{z}}{{log}\left(\frac{\mathrm{1}+{z}}{\mathrm{1}−{z}}\right)}=\frac{{z}}{\mathrm{2}\left({z}+\frac{{z}^{\mathrm{3}} }{\mathrm{3}}+..\right)}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${log}\left(\frac{\mathrm{1}+{z}}{\mathrm{1}−{z}}\right)={z}−\frac{{z}^{\mathrm{2}} }{\mathrm{2}}+\frac{{z}^{\mathrm{3}} }{\mathrm{3}}−..+\left({z}+\frac{{z}^{\mathrm{2}} }{\mathrm{2}}+..\right)=\mathrm{2}\left({z}+\frac{{z}^{\mathrm{3}} }{\mathrm{3}}+..\right) \\ $$

Answered by mnjuly1970 last updated on 14/Jun/21

solution: Φ:=lim_(x→1) ((x−1)/(ln((x/(2−x)))))=^(⟨x−1= t ⟩) lim_(t→0) ((t/(ln(((t+1)/(1−t)))))) :=lim_(t→0) ((t/(ln(1+t)−ln(1−t)))) :=lim_(t→0) ((t/(t−(t^2 /2)+...−(−t−(t^2 /2)...)))) :≈lim_(t→0) (t/(2t)) =(1/2) ......... Φ:=(1/2)

$$\:{solution}: \\ $$$$\:\:\:\:\:\Phi:={lim}_{{x}\rightarrow\mathrm{1}} \frac{{x}−\mathrm{1}}{{ln}\left(\frac{{x}}{\mathrm{2}−{x}}\right)}\overset{\langle{x}−\mathrm{1}=\:{t}\:\rangle} {=}{lim}_{{t}\rightarrow\mathrm{0}} \left(\frac{{t}}{{ln}\left(\frac{{t}+\mathrm{1}}{\mathrm{1}−{t}}\right)}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\::={lim}_{{t}\rightarrow\mathrm{0}} \left(\frac{{t}}{{ln}\left(\mathrm{1}+{t}\right)−{ln}\left(\mathrm{1}−{t}\right)}\right) \\ $$$$\:\:\:\:\:\::={lim}_{{t}\rightarrow\mathrm{0}} \left(\frac{{t}}{{t}−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}+…−\left(−{t}−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}…\right)}\right) \\ $$$$\:\:\:\:\:\:\::\approx{lim}_{{t}\rightarrow\mathrm{0}} \frac{{t}}{\mathrm{2}{t}}\:=\frac{\mathrm{1}}{\mathrm{2}}\:………\:\:\:\Phi:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Answered by mathmax by abdo last updated on 14/Jun/21

f(x)=((x−1)/(log((x/(2−x))))) ⇒f(x)=((x−1)/(logx−log(2−x))) changement x−1=t give f(x)=(t/(log(1+t)−log(2−t−1)))=Ψ(t) (t→0) =(t/(log(1+t)−log(1−t))) log^′ (1+t)=(1/(1+t))=1−t +o(t) ⇒log(1+t)=t−(t^2 /2) +o(t^2 ) also log(1−t)=−t−(t^2 /2)+o(t^2 ) ⇒ Ψ(t)∼(t/(t−(t^2 /2)+t+(t^2 /2)))=(t/(2t))=(1/2) ⇒lim_(t→0) Ψ(t)=(1/2) ⇒lim_(x→1) f(x)=(1/2)

$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{x}−\mathrm{1}}{\mathrm{log}\left(\frac{\mathrm{x}}{\mathrm{2}−\mathrm{x}}\right)}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{x}−\mathrm{1}}{\mathrm{logx}−\mathrm{log}\left(\mathrm{2}−\mathrm{x}\right)} \\ $$$$\mathrm{changement}\:\mathrm{x}−\mathrm{1}=\mathrm{t}\:\mathrm{give}\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{t}}{\mathrm{log}\left(\mathrm{1}+\mathrm{t}\right)−\mathrm{log}\left(\mathrm{2}−\mathrm{t}−\mathrm{1}\right)}=\Psi\left(\mathrm{t}\right)\:\:\left(\mathrm{t}\rightarrow\mathrm{0}\right) \\ $$$$=\frac{\mathrm{t}}{\mathrm{log}\left(\mathrm{1}+\mathrm{t}\right)−\mathrm{log}\left(\mathrm{1}−\mathrm{t}\right)} \\ $$$$\mathrm{log}^{'} \left(\mathrm{1}+\mathrm{t}\right)=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{t}}=\mathrm{1}−\mathrm{t}\:+\mathrm{o}\left(\mathrm{t}\right)\:\Rightarrow\mathrm{log}\left(\mathrm{1}+\mathrm{t}\right)=\mathrm{t}−\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}\:+\mathrm{o}\left(\mathrm{t}^{\mathrm{2}} \right)\:\mathrm{also} \\ $$$$\mathrm{log}\left(\mathrm{1}−\mathrm{t}\right)=−\mathrm{t}−\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{o}\left(\mathrm{t}^{\mathrm{2}} \right)\:\Rightarrow \\ $$$$\Psi\left(\mathrm{t}\right)\sim\frac{\mathrm{t}}{\mathrm{t}−\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{t}+\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}}=\frac{\mathrm{t}}{\mathrm{2t}}=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\mathrm{lim}_{\mathrm{t}\rightarrow\mathrm{0}} \Psi\left(\mathrm{t}\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{1}} \mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Facebook Tweet Pin

lim-x-1-x-1-ln-x-2-x-

Leave a Reply Cancel reply