Question Number 67031 by hmamarques1994@gmai.com last updated on 21/Aug/19

$$\: \\ $$$$\:\underset{\boldsymbol{\mathrm{x}}\rightarrow−\mathrm{1}} {\boldsymbol{\mathrm{lim}}}\sqrt[{\mathrm{3}}]{\frac{\sqrt[{\mathrm{7}}]{\boldsymbol{\mathrm{x}}^{\mathrm{5}} }+\mathrm{1}}{\mathrm{1}+\sqrt[{\mathrm{9}\:}]{\boldsymbol{\mathrm{x}}^{\mathrm{7}} }}}=? \\ $$$$\: \\ $$
Commented by Tony Lin last updated on 22/Aug/19
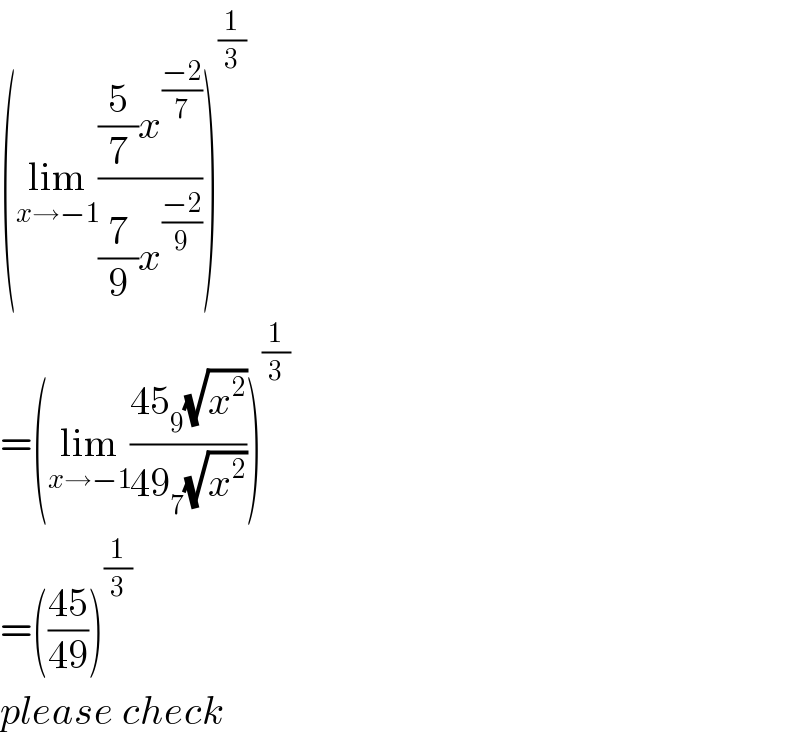
$$\left(\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}\frac{\frac{\mathrm{5}}{\mathrm{7}}{x}^{\frac{−\mathrm{2}}{\mathrm{7}}} }{\frac{\mathrm{7}}{\mathrm{9}}{x}^{\frac{−\mathrm{2}}{\mathrm{9}}} }\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$=\left(\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{45}_{\mathrm{9}} \sqrt{{x}^{\mathrm{2}} }}{\mathrm{49}_{\mathrm{7}} \sqrt{{x}^{\mathrm{2}} }}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$=\left(\frac{\mathrm{45}}{\mathrm{49}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$${please}\:{check} \\ $$
Commented by hmamarques1994@gmail.com last updated on 22/Aug/19
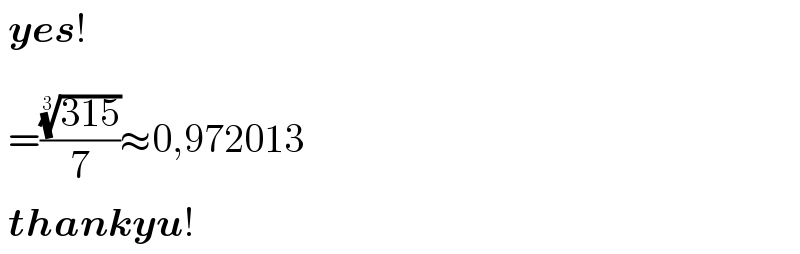
$$\:\boldsymbol{{yes}}\underset{\:} {!} \\ $$$$\:=\frac{\sqrt[{\mathrm{3}}]{\mathrm{315}}}{\mathrm{7}}\approx\mathrm{0},\mathrm{972013} \\ $$$$\:\boldsymbol{{thankyu}}! \\ $$
Commented by mathmax by abdo last updated on 22/Aug/19
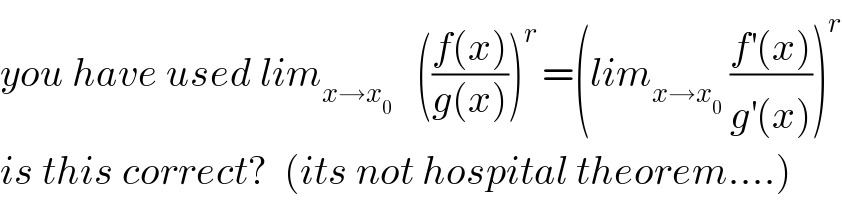
$${you}\:{have}\:{used}\:{lim}_{{x}\rightarrow{x}_{\mathrm{0}} } \:\:\:\left(\frac{{f}\left({x}\right)}{{g}\left({x}\right)}\right)^{{r}\:} =\left({lim}_{{x}\rightarrow{x}_{\mathrm{0}} } \:\frac{{f}^{'} \left({x}\right)}{{g}^{'} \left({x}\right)}\right)^{{r}} \\ $$$${is}\:{this}\:{correct}?\:\:\left({its}\:{not}\:{hospital}\:{theorem}….\right) \\ $$
Commented by Tony Lin last updated on 22/Aug/19
![L′Hospital rule: if lim_(x→x_0 ) f(x)=lim_(x→x_0 ) g(x)=0 and lim_(x→x_0 ) ((f′(x))/(g′(x))) exists ⇒lim_(x→x_0 ) ((f(x))/(g(x)))=lim_(x→x_0 ) ((f′(x))/(g′(x))) if lim_(x→x_0 ) f(x)=±∞, lim_(x→x_0 ) g(x)=±∞ and lim_(x→x_0 ) ((f′(x))/(g′(x))) exists ⇒lim_(x→x_0 ) ((f(x))/(g(x)))=lim_(x→x_0 ) ((f′(x))/(g′(x))) if lim_(x→x_0 ) f(x) exists lim_(x→x_0 ) [f(x)]^n =[lim_(x→x_0 ) f(x)]^n ⇒Power Law of Limit or we can use Composition Law to know if f is continuous at lim_(x→x_0 ) g(x) then lim_(x→x_0 ) f(g(x))=f(lim_(x→x_0 ) g(x))](https://www.tinkutara.com/question/Q67094.png)
$${L}'{Hospital}\:{rule}: \\ $$$${if}\:\underset{{x}\rightarrow{x}_{\mathrm{0}} } {\mathrm{lim}}{f}\left({x}\right)=\underset{{x}\rightarrow{x}_{\mathrm{0}} } {\mathrm{lim}}{g}\left({x}\right)=\mathrm{0}\:{and}\:\underset{{x}\rightarrow{x}_{\mathrm{0}} } {\mathrm{lim}}\frac{{f}'\left({x}\right)}{{g}'\left({x}\right)}\:{exists} \\ $$$$\Rightarrow\underset{{x}\rightarrow{x}_{\mathrm{0}} } {\mathrm{lim}}\frac{{f}\left({x}\right)}{{g}\left({x}\right)}=\underset{{x}\rightarrow{x}_{\mathrm{0}} } {\mathrm{lim}}\frac{{f}'\left({x}\right)}{{g}'\left({x}\right)} \\ $$$${if}\:\underset{{x}\rightarrow{x}_{\mathrm{0}} } {\mathrm{lim}}{f}\left({x}\right)=\pm\infty,\:\underset{{x}\rightarrow{x}_{\mathrm{0}} } {\mathrm{lim}}{g}\left({x}\right)=\pm\infty\:{and}\:\underset{{x}\rightarrow{x}_{\mathrm{0}} } {\mathrm{lim}}\frac{{f}'\left({x}\right)}{{g}'\left({x}\right)}\:{exists} \\ $$$$\Rightarrow\underset{{x}\rightarrow{x}_{\mathrm{0}} } {\mathrm{lim}}\frac{{f}\left({x}\right)}{{g}\left({x}\right)}=\underset{{x}\rightarrow{x}_{\mathrm{0}} } {\mathrm{lim}}\frac{{f}'\left({x}\right)}{{g}'\left({x}\right)} \\ $$$${if}\:\underset{{x}\rightarrow{x}_{\mathrm{0}} } {\mathrm{lim}}{f}\left({x}\right)\:{exists} \\ $$$$\underset{{x}\rightarrow{x}_{\mathrm{0}} } {\mathrm{lim}}\left[{f}\left({x}\right)\right]^{{n}} =\left[\underset{{x}\rightarrow{x}_{\mathrm{0}} } {\mathrm{lim}}{f}\left({x}\right)\right]^{{n}} \\ $$$$\Rightarrow{Power}\:{Law}\:{of}\:{Limit} \\ $$$${or}\:{we}\:{can}\:{use}\:{Composition}\:{Law}\:{to}\:{know} \\ $$$${if}\:{f}\:{is}\:{continuous}\:{at}\:\underset{{x}\rightarrow{x}_{\mathrm{0}} } {\mathrm{lim}}{g}\left({x}\right) \\ $$$${then}\:\underset{{x}\rightarrow{x}_{\mathrm{0}} } {\mathrm{lim}}{f}\left({g}\left({x}\right)\right)={f}\left(\underset{{x}\rightarrow{x}_{\mathrm{0}} } {\mathrm{lim}}{g}\left({x}\right)\right) \\ $$
