Menu Close

lim-x-1-x-50-8x-7-x-20-5x-6-

Tinku Tara 0 Comments
Pin




Question Number 141961 by iloveisrael last updated on 25/May/21
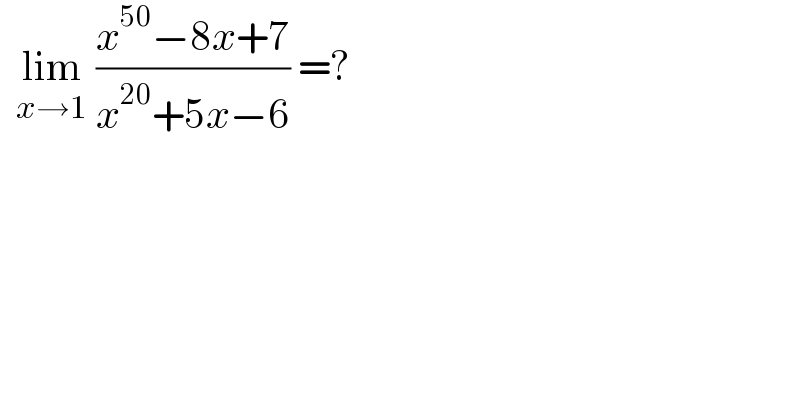
lim_(x→1) ((x^(50) −8x+7)/(x^(20) +5x−6)) =?
$$\:\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{50}} −\mathrm{8}{x}+\mathrm{7}}{{x}^{\mathrm{20}} +\mathrm{5}{x}−\mathrm{6}}\:=? \\ $$
Answered by iloveisrael last updated on 25/May/21
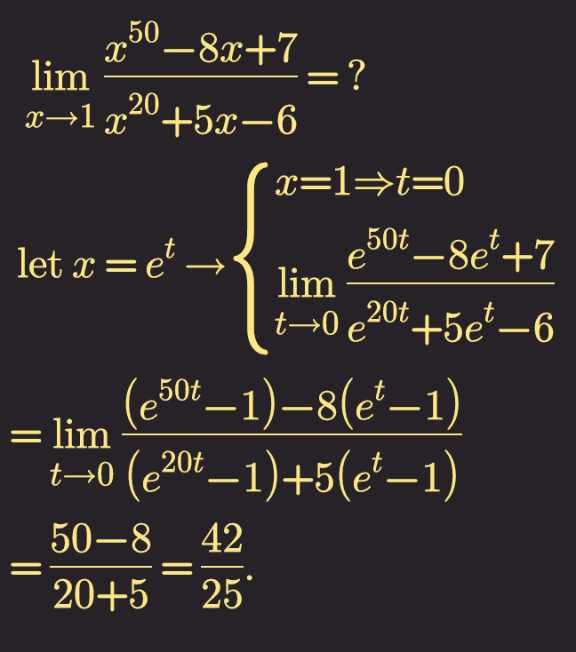
Answered by Panacea last updated on 25/May/21
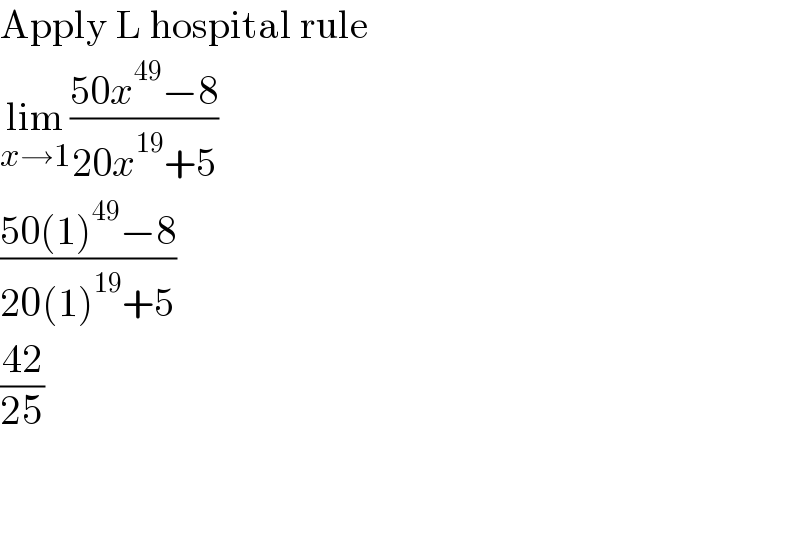
Apply L hospital rule lim_(x→1) ((50x^(49) −8)/(20x^(19) +5)) ((50(1)^(49) −8)/(20(1)^(19) +5)) ((42)/(25))
$$\mathrm{Apply}\:\mathrm{L}\:\mathrm{hospital}\:\mathrm{rule} \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{50}{x}^{\mathrm{49}} −\mathrm{8}}{\mathrm{20}{x}^{\mathrm{19}} +\mathrm{5}} \\ $$$$\frac{\mathrm{50}\left(\mathrm{1}\right)^{\mathrm{49}} −\mathrm{8}}{\mathrm{20}\left(\mathrm{1}\right)^{\mathrm{19}} +\mathrm{5}} \\ $$$$\frac{\mathrm{42}}{\mathrm{25}} \\ $$$$ \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 25/May/21
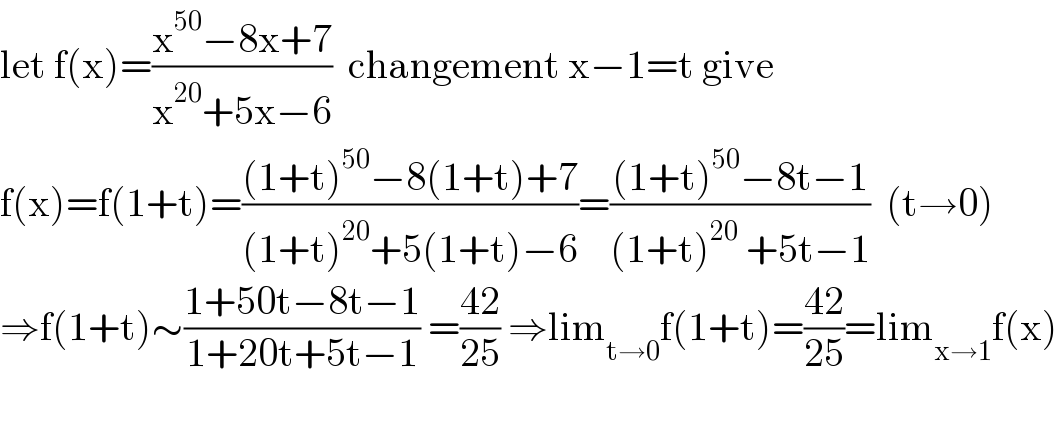
let f(x)=((x^(50) −8x+7)/(x^(20) +5x−6)) changement x−1=t give f(x)=f(1+t)=(((1+t)^(50) −8(1+t)+7)/((1+t)^(20) +5(1+t)−6))=(((1+t)^(50) −8t−1)/((1+t)^(20) +5t−1)) (t→0) ⇒f(1+t)∼((1+50t−8t−1)/(1+20t+5t−1)) =((42)/(25)) ⇒lim_(t→0) f(1+t)=((42)/(25))=lim_(x→1) f(x)
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{x}^{\mathrm{50}} −\mathrm{8x}+\mathrm{7}}{\mathrm{x}^{\mathrm{20}} +\mathrm{5x}−\mathrm{6}}\:\:\mathrm{changement}\:\mathrm{x}−\mathrm{1}=\mathrm{t}\:\mathrm{give} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{f}\left(\mathrm{1}+\mathrm{t}\right)=\frac{\left(\mathrm{1}+\mathrm{t}\right)^{\mathrm{50}} −\mathrm{8}\left(\mathrm{1}+\mathrm{t}\right)+\mathrm{7}}{\left(\mathrm{1}+\mathrm{t}\right)^{\mathrm{20}} +\mathrm{5}\left(\mathrm{1}+\mathrm{t}\right)−\mathrm{6}}=\frac{\left(\mathrm{1}+\mathrm{t}\right)^{\mathrm{50}} −\mathrm{8t}−\mathrm{1}}{\left(\mathrm{1}+\mathrm{t}\right)^{\mathrm{20}} \:+\mathrm{5t}−\mathrm{1}}\:\:\left(\mathrm{t}\rightarrow\mathrm{0}\right) \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{1}+\mathrm{t}\right)\sim\frac{\mathrm{1}+\mathrm{50t}−\mathrm{8t}−\mathrm{1}}{\mathrm{1}+\mathrm{20t}+\mathrm{5t}−\mathrm{1}}\:=\frac{\mathrm{42}}{\mathrm{25}}\:\Rightarrow\mathrm{lim}_{\mathrm{t}\rightarrow\mathrm{0}} \mathrm{f}\left(\mathrm{1}+\mathrm{t}\right)=\frac{\mathrm{42}}{\mathrm{25}}=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{1}} \mathrm{f}\left(\mathrm{x}\right) \\ $$$$ \\ $$
Answered by mnjuly1970 last updated on 25/May/21
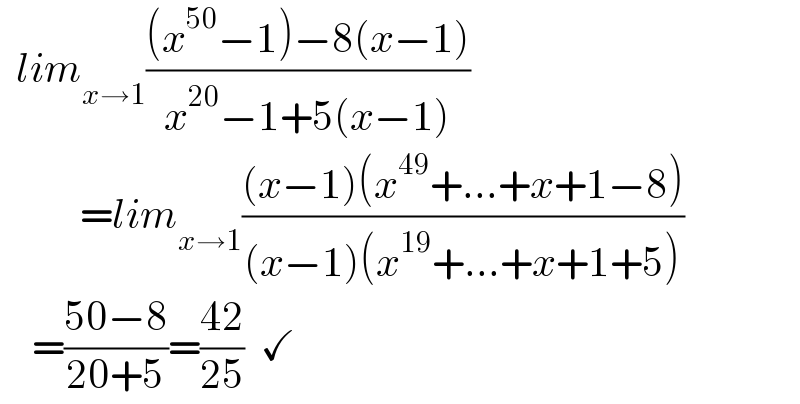
lim_(x→1) (((x^(50) −1)−8(x−1))/(x^(20) −1+5(x−1))) =lim_(x→1) (((x−1)(x^(49) +...+x+1−8))/((x−1)(x^(19) +...+x+1+5))) =((50−8)/(20+5))=((42)/(25)) ✓
$$\:\:{lim}_{{x}\rightarrow\mathrm{1}} \frac{\left({x}^{\mathrm{50}} −\mathrm{1}\right)−\mathrm{8}\left({x}−\mathrm{1}\right)}{{x}^{\mathrm{20}} −\mathrm{1}+\mathrm{5}\left({x}−\mathrm{1}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:={lim}_{{x}\rightarrow\mathrm{1}} \frac{\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{49}} +…+{x}+\mathrm{1}−\mathrm{8}\right)}{\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{19}} +…+{x}+\mathrm{1}+\mathrm{5}\right)} \\ $$$$\:\:\:\:=\frac{\mathrm{50}−\mathrm{8}}{\mathrm{20}+\mathrm{5}}=\frac{\mathrm{42}}{\mathrm{25}}\:\:\checkmark \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *