lim-x-2-log-x-2-1-log-2-1-x-1-

Question Number 66478 by hmamarques1994@gmail.com last updated on 15/Aug/19

$$\: \\ $$$$\:\underset{\boldsymbol{{x}}\rightarrow\mathrm{2}} {\boldsymbol{{lim}}}\left[\frac{\boldsymbol{{log}}_{\boldsymbol{{x}}} \left(\mathrm{2}\right)−\mathrm{1}}{\boldsymbol{{log}}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\boldsymbol{{x}}}\right)+\mathrm{1}}\right]=? \\ $$$$\: \\ $$

Commented by gunawan last updated on 16/Aug/19

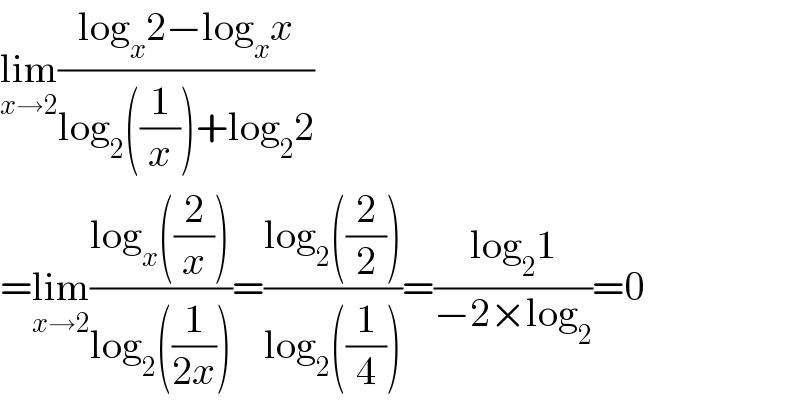
$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{\mathrm{log}_{{x}} \mathrm{2}−\mathrm{log}_{{x}} {x}}{\mathrm{log}_{\mathrm{2}} \left(\frac{\mathrm{1}}{{x}}\right)+\mathrm{log}_{\mathrm{2}} \mathrm{2}} \\ $$$$=\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{\mathrm{log}_{{x}} \left(\frac{\mathrm{2}}{{x}}\right)}{\mathrm{log}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}{x}}\right)}=\frac{\mathrm{log}_{\mathrm{2}} \left(\frac{\mathrm{2}}{\mathrm{2}}\right)}{\mathrm{log}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)}=\frac{\mathrm{log}_{\mathrm{2}} \mathrm{1}}{−\mathrm{2}×\mathrm{log}_{\mathrm{2}} }=\mathrm{0} \\ $$

Commented by Rasheed.Sindhi last updated on 16/Aug/19

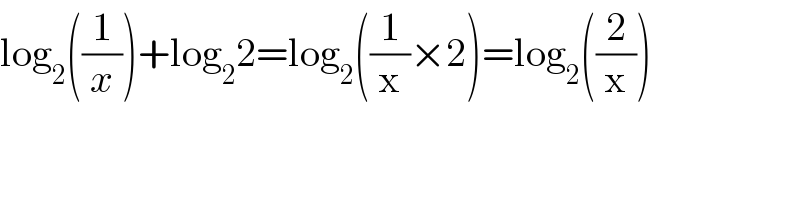
$$\mathrm{log}_{\mathrm{2}} \left(\frac{\mathrm{1}}{{x}}\right)+\mathrm{log}_{\mathrm{2}} \mathrm{2}=\mathrm{log}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{x}}×\mathrm{2}\right)=\mathrm{log}_{\mathrm{2}} \left(\frac{\mathrm{2}}{\mathrm{x}}\right) \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com