Question Number 69255 by TawaTawa last updated on 21/Sep/19

$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\:\sqrt{\frac{\mathrm{x}^{\mathrm{3}} \:−\:\mathrm{4}}{\mathrm{x}^{\mathrm{2}} \:−\:\mathrm{3x}\:+\:\mathrm{2}}} \\ $$
Answered by Henri Boucatchou last updated on 21/Sep/19

$$\underset{\boldsymbol{{x}}\rightarrow\mathrm{2}} {\boldsymbol{{lim}}}\sqrt{\frac{\boldsymbol{{x}}^{\mathrm{3}} −\mathrm{4}}{\boldsymbol{{x}}^{\mathrm{2}} −\mathrm{3}\boldsymbol{{x}}+\mathrm{2}}}\:=\:\sqrt{\frac{\mathrm{4}}{\mathrm{0}}}=\:\infty; \\ $$$$\boldsymbol{{but}}\:\:\underset{\boldsymbol{{x}}\rightarrow\mathrm{2}} {\boldsymbol{{lim}}}\sqrt{\frac{\boldsymbol{{x}}^{\mathrm{2}} −\mathrm{4}}{\boldsymbol{{x}}^{\mathrm{2}} −\mathrm{3}\boldsymbol{{x}}+\mathrm{2}}}\:=\:\underset{\boldsymbol{{x}}\rightarrow\mathrm{2}} {\boldsymbol{{lim}}}\sqrt{\frac{\boldsymbol{{x}}+\mathrm{2}}{\boldsymbol{{x}}−\mathrm{1}}}\:=\:\mathrm{2}. \\ $$
Commented by malwaan last updated on 21/Sep/19

$$\underset{\boldsymbol{{x}}\rightarrow\mathrm{2}} {\boldsymbol{{lim}}}\sqrt{\frac{\boldsymbol{{x}}^{\mathrm{3}} −\mathrm{8}}{\boldsymbol{{x}}^{\mathrm{2}} −\mathrm{3}\boldsymbol{{x}}+\mathrm{2}}\:}\:=\:\underset{\boldsymbol{{x}}\rightarrow\mathrm{2}} {\boldsymbol{{lim}}}\sqrt{\frac{\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{2}\boldsymbol{{x}}+\mathrm{4}}{\boldsymbol{{x}}−\mathrm{1}}} \\ $$$$\sqrt{\mathrm{12}}\:=\:\mathrm{2}\sqrt{\mathrm{3}} \\ $$
Commented by mathmax by abdo last updated on 22/Sep/19

$${perhaps}\:{the}\:{question}\:{is}\:{find}\:{lim}_{{x}\rightarrow\mathrm{2}} \:\sqrt{\frac{{x}^{\mathrm{3}} −\mathrm{8}}{{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}}} \\ $$$${we}\:{have}\:{x}^{\mathrm{3}} −\mathrm{8}\:=\left({x}−\mathrm{2}\right)\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{4}\right)\:{and} \\ $$$${x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}\:={x}^{\mathrm{2}} −\mathrm{2}{x}−\left({x}−\mathrm{2}\right)\:={x}\left({x}−\mathrm{2}\right)−\left({x}−\mathrm{2}\right) \\ $$$$=\left({x}−\mathrm{2}\right)\left({x}−\mathrm{1}\right)\:\Rightarrow\frac{{x}^{\mathrm{3}} −\mathrm{8}}{{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}}\:=\frac{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{4}}{{x}−\mathrm{1}}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{2}} \sqrt{\left(…\right)}={lim}_{{x}\rightarrow\mathrm{2}} \sqrt{\frac{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{4}}{{x}−\mathrm{1}}}=\sqrt{\mathrm{12}}=\mathrm{2}\sqrt{\mathrm{3}} \\ $$
Commented by TawaTawa last updated on 22/Sep/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by TawaTawa last updated on 22/Sep/19
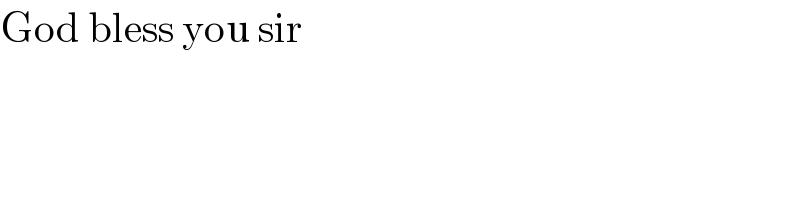
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by mathmax by abdo last updated on 22/Sep/19

$${you}\:{are}\:{welcome}\:{sir}. \\ $$
