Question Number 136258 by EDWIN88 last updated on 20/Mar/21
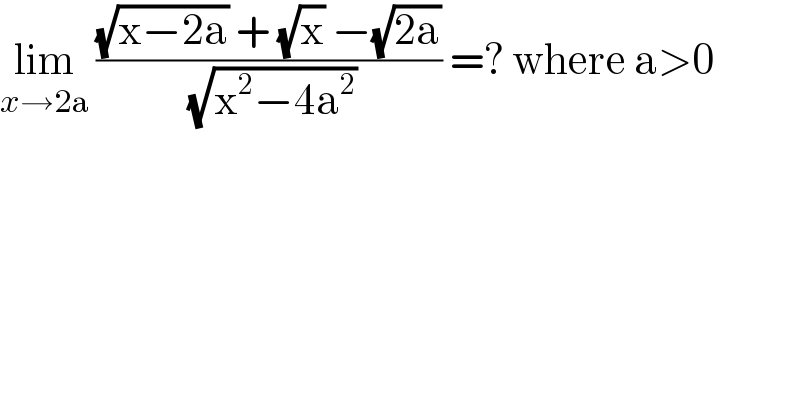
$$\underset{{x}\rightarrow\mathrm{2a}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{x}−\mathrm{2a}}\:+\:\sqrt{\mathrm{x}}\:−\sqrt{\mathrm{2a}}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{4a}^{\mathrm{2}} }}\:=?\:\mathrm{where}\:\mathrm{a}>\mathrm{0} \\ $$
Answered by liberty last updated on 20/Mar/21

$$\:{L}'{H}\ddot {{o}pital}\: \\ $$$$=\:\underset{{x}\rightarrow\mathrm{2}{a}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\:\sqrt{{x}+\mathrm{2}{a}}}\:.\underset{{x}\rightarrow\mathrm{2}{a}} {\mathrm{lim}}\:\frac{\sqrt{{x}−\mathrm{2}{a}}\:+\sqrt{{x}}−\sqrt{\mathrm{2}{a}}}{\:\sqrt{{x}−\mathrm{2}{a}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{a}}}\:.\underset{{x}\rightarrow\mathrm{2}{a}} {\mathrm{lim}}\:\frac{\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}−\mathrm{2}{a}}}\:+\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}}{\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}−\mathrm{2}{a}}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{a}}}\:.\underset{{x}\rightarrow\mathrm{2}{a}} {\mathrm{lim}}\:\left(\frac{\sqrt{{x}}\:+\sqrt{{x}−\mathrm{2}{a}}}{\:\sqrt{{x}}\:\sqrt{{x}−\mathrm{2}{a}}}\right).\sqrt{{x}−\mathrm{2}{a}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{a}}}\:.\underset{{x}\rightarrow\mathrm{2}{a}} {\mathrm{lim}}\:\left(\frac{\sqrt{{x}}\:+\sqrt{{x}−\mathrm{2}{a}}}{\:\sqrt{{x}}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{a}}}.\:\frac{\sqrt{\mathrm{2}{a}}\:+\mathrm{0}}{\:\sqrt{\mathrm{2}{a}}}\:=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{{a}}} \\ $$
Answered by EDWIN88 last updated on 20/Mar/21

$$\mathrm{Without}\:\mathrm{L}'\mathrm{H}\ddot {\mathrm{o}pital}\: \\ $$$$\underset{{x}\rightarrow\mathrm{2a}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{x}+\mathrm{2a}}}\:.\underset{{x}\rightarrow\mathrm{2a}} {\mathrm{lim}}\:\frac{\left(\sqrt{\mathrm{x}−\mathrm{2a}}\:+\left(\sqrt{\mathrm{x}}\:−\sqrt{\mathrm{2a}}\:\right)\right.}{\:\sqrt{\mathrm{x}−\mathrm{2a}}}\: \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{a}}}\:.\underset{{x}\rightarrow\mathrm{2a}} {\mathrm{lim}}\:\left(\mathrm{1}+\:\frac{\sqrt{\mathrm{x}}−\sqrt{\mathrm{2a}}}{\:\sqrt{\mathrm{x}−\mathrm{2a}}}\:\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{a}}}\:.\left(\mathrm{1}+\underset{{x}\rightarrow\mathrm{2a}} {\mathrm{lim}}\:\frac{\mathrm{x}−\mathrm{2a}}{\left(\sqrt{\mathrm{x}}+\sqrt{\mathrm{2a}}\:\right)\sqrt{\mathrm{x}−\mathrm{2a}}}\:\right)\: \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{a}}}\:.\left(\mathrm{1}+\:\underset{{x}\rightarrow\mathrm{2a}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{x}−\mathrm{2a}}}{\:\sqrt{\mathrm{x}}\:+\sqrt{\mathrm{2a}}}\:\right)=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{a}}}.\left(\mathrm{1}+\mathrm{0}\right) \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{a}}}\:. \\ $$
