lim-x-4-2-x-x-1-3-2-8-x-x-

Question Number 66640 by hmamarques1994@gmail.com last updated on 18/Aug/19

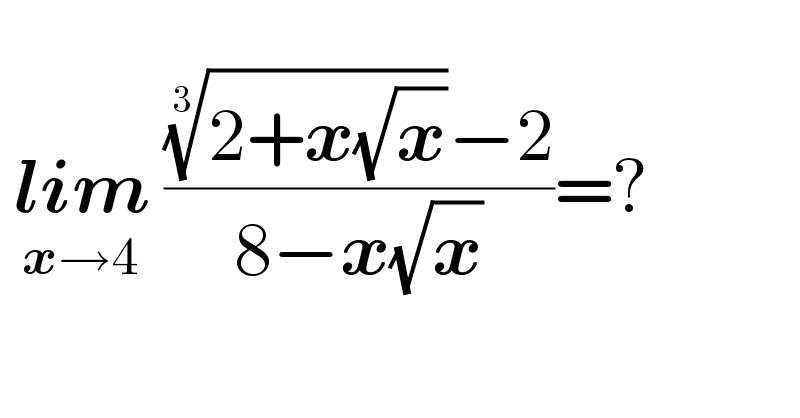
$$\: \\ $$$$\:\underset{\boldsymbol{{x}}\rightarrow\mathrm{4}} {\boldsymbol{{lim}}}\:\frac{\sqrt[{\mathrm{3}}]{\mathrm{2}+\boldsymbol{{x}}\sqrt{\boldsymbol{{x}}}}−\mathrm{2}}{\mathrm{8}−\boldsymbol{{x}}\sqrt{\boldsymbol{{x}}}}=? \\ $$$$\: \\ $$

Commented by kaivan.ahmadi last updated on 18/Aug/19

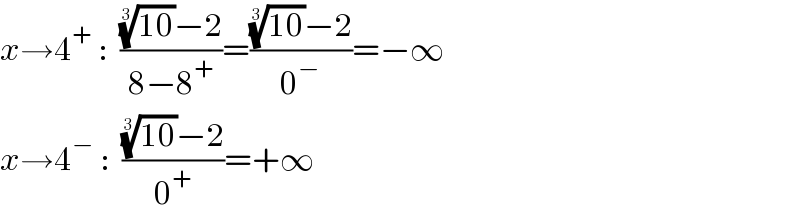
x→4^+ : ((((10))^(1/3) −2)/(8−8^+ ))=((((10))^(1/3) −2)/0^− )=−∞ x→4^− : ((((10))^(1/3) −2)/0^+ )=+∞

$${x}\rightarrow\mathrm{4}^{+} \::\:\:\frac{\sqrt[{\mathrm{3}}]{\mathrm{10}}−\mathrm{2}}{\mathrm{8}−\mathrm{8}^{+} }=\frac{\sqrt[{\mathrm{3}}]{\mathrm{10}}−\mathrm{2}}{\mathrm{0}^{−} }=−\infty \\ $$$${x}\rightarrow\mathrm{4}^{−} \::\:\:\frac{\sqrt[{\mathrm{3}}]{\mathrm{10}}−\mathrm{2}}{\mathrm{0}^{+} }=+\infty \\ $$

Commented by kaivan.ahmadi last updated on 18/Aug/19

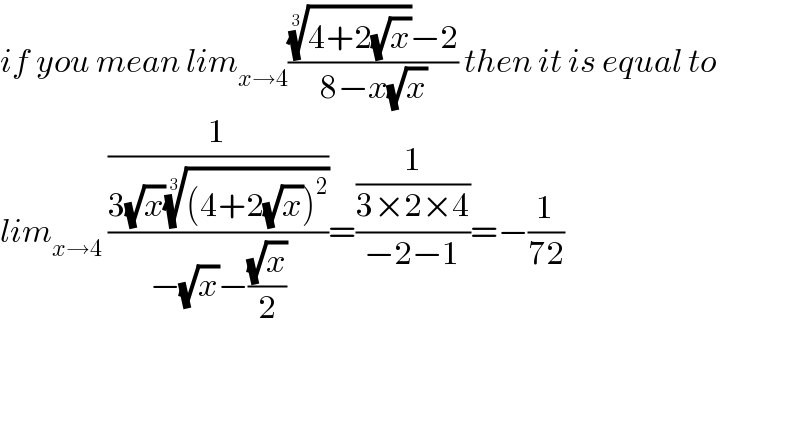
if you mean lim_(x→4) ((((4+2(√x)))^(1/3) −2)/(8−x(√x))) then it is equal to lim_(x→4) ((1/(3(√x)(((4+2(√x))^2 ))^(1/3) ))/(−(√x)−((√x)/2)))=((1/(3×2×4))/(−2−1))=−(1/(72))

$${if}\:{you}\:{mean}\:{lim}_{{x}\rightarrow\mathrm{4}} \frac{\sqrt[{\mathrm{3}}]{\mathrm{4}+\mathrm{2}\sqrt{{x}}}−\mathrm{2}}{\mathrm{8}−{x}\sqrt{{x}}}\:{then}\:{it}\:{is}\:{equal}\:{to} \\ $$$${lim}_{{x}\rightarrow\mathrm{4}} \:\frac{\frac{\mathrm{1}}{\mathrm{3}\sqrt{{x}}\sqrt[{\mathrm{3}}]{\left(\mathrm{4}+\mathrm{2}\sqrt{{x}}\right)^{\mathrm{2}} }}}{−\sqrt{{x}}−\frac{\sqrt{{x}}}{\mathrm{2}}}=\frac{\frac{\mathrm{1}}{\mathrm{3}×\mathrm{2}×\mathrm{4}}}{−\mathrm{2}−\mathrm{1}}=−\frac{\mathrm{1}}{\mathrm{72}} \\ $$$$ \\ $$$$ \\ $$

Commented by mathmax by abdo last updated on 18/Aug/19

perhaps the Q is find lim_(x→4) (((^3 (√(x(√x)))−2)/(8−x(√x))) or lim_(x→4) (((^3 (√(4+2(√x)))−2)/(8−x(√x))) let find lim_(x→4) (((^3 (√(x(√x)))−2)/(8−x(√x))) =lim_(x→4) A(x) changement (^3 (√(x(√x))))=t give x(√x)=t^3 ⇒lim_(x→4) A(x)=lim_(t→2) ((t−2)/(8−t^3 )) =−lim_(t→2) ((t−2)/((t−2)(t^2 +2t +4))) =lim_(t→2) ((−1)/(t^2 +2t +4)) =((−1)/(12)) let find lim_(x→4) (((^3 (√(4+2(√x)))−2)/(8−x(√x)))=lim_(x→4) B(x) we dl the changement (^3 (√(4+2(√x))))=t ⇒4+2(√x)=t^3 ⇒2(√x)=t^3 −4 ⇒(√x) =(t^3 /2)−2 ⇒ x=((t^3 /2)−2)^2 ⇒lim_(x→4) B(x) =lim_(t→2) ((t−2)/(8−((t^3 /2)−2)^3 )) =lim_(t→2) ((t−2)/(8−(((t^3 −4)/2))^3 )) =lim_(t→2) 8× ((t−2)/(64−(t^3 −4)^3 )) =lim_(t→2) ((8(t−2))/(64−(t^9 −3t^6 (4)+3t^3 4^2 −4^3 ))) =lim_(t→2) ((8(t−2))/(64−t^9 +12t^6 −48t^3 +64)) =lim_(t→2) ((8(t−2))/(−t^9 +12t^6 −48t^3 +128)) =_(hop) lim_(t→2) (8/(−9t^8 +12×6t^5 −48×3 t^2 )) =(8/(−9.2^8 +12×6. 2^5 −48.3.2^2 )) =.....

$${perhaps}\:{the}\:{Q}\:{is}\:{find}\:{lim}_{{x}\rightarrow\mathrm{4}} \frac{\left(^{\mathrm{3}} \sqrt{{x}\sqrt{{x}}}−\mathrm{2}\right.}{\mathrm{8}−{x}\sqrt{{x}}}\:\:{or}\:{lim}_{{x}\rightarrow\mathrm{4}} \:\:\frac{\left(^{\mathrm{3}} \sqrt{\mathrm{4}+\mathrm{2}\sqrt{{x}}}−\mathrm{2}\right.}{\mathrm{8}−{x}\sqrt{{x}}} \\ $$$${let}\:{find}\:{lim}_{{x}\rightarrow\mathrm{4}} \:\:\:\frac{\left(^{\mathrm{3}} \sqrt{{x}\sqrt{{x}}}−\mathrm{2}\right.}{\mathrm{8}−{x}\sqrt{{x}}}\:\:={lim}_{{x}\rightarrow\mathrm{4}} \:{A}\left({x}\right)\:{changement} \\ $$$$\left(^{\mathrm{3}} \sqrt{{x}\sqrt{{x}}}\right)={t}\:{give}\:{x}\sqrt{{x}}={t}^{\mathrm{3}} \:\Rightarrow{lim}_{{x}\rightarrow\mathrm{4}} \:{A}\left({x}\right)={lim}_{{t}\rightarrow\mathrm{2}} \:\:\:\:\frac{{t}−\mathrm{2}}{\mathrm{8}−{t}^{\mathrm{3}} } \\ $$$$=−{lim}_{{t}\rightarrow\mathrm{2}} \:\:\frac{{t}−\mathrm{2}}{\left({t}−\mathrm{2}\right)\left({t}^{\mathrm{2}} \:+\mathrm{2}{t}\:+\mathrm{4}\right)}\:={lim}_{{t}\rightarrow\mathrm{2}} \:\:\:\:\frac{−\mathrm{1}}{{t}^{\mathrm{2}} \:+\mathrm{2}{t}\:+\mathrm{4}}\:=\frac{−\mathrm{1}}{\mathrm{12}} \\ $$$${let}\:{find}\:{lim}_{{x}\rightarrow\mathrm{4}} \:\frac{\left(^{\mathrm{3}} \sqrt{\mathrm{4}+\mathrm{2}\sqrt{{x}}}−\mathrm{2}\right.}{\mathrm{8}−{x}\sqrt{{x}}}={lim}_{{x}\rightarrow\mathrm{4}} {B}\left({x}\right)\:\:\:{we}\:{dl}\:{the}\:{changement}\: \\ $$$$\left(^{\mathrm{3}} \sqrt{\mathrm{4}+\mathrm{2}\sqrt{{x}}}\right)={t}\:\Rightarrow\mathrm{4}+\mathrm{2}\sqrt{{x}}={t}^{\mathrm{3}} \:\Rightarrow\mathrm{2}\sqrt{{x}}={t}^{\mathrm{3}} −\mathrm{4}\:\Rightarrow\sqrt{{x}}\:=\frac{{t}^{\mathrm{3}} }{\mathrm{2}}−\mathrm{2}\:\Rightarrow \\ $$$${x}=\left(\frac{{t}^{\mathrm{3}} }{\mathrm{2}}−\mathrm{2}\right)^{\mathrm{2}} \:\Rightarrow{lim}_{{x}\rightarrow\mathrm{4}} \:{B}\left({x}\right)\:={lim}_{{t}\rightarrow\mathrm{2}} \:\:\:\:\frac{{t}−\mathrm{2}}{\mathrm{8}−\left(\frac{{t}^{\mathrm{3}} }{\mathrm{2}}−\mathrm{2}\right)^{\mathrm{3}} } \\ $$$$={lim}_{{t}\rightarrow\mathrm{2}} \:\:\frac{{t}−\mathrm{2}}{\mathrm{8}−\left(\frac{{t}^{\mathrm{3}} −\mathrm{4}}{\mathrm{2}}\right)^{\mathrm{3}} }\:={lim}_{{t}\rightarrow\mathrm{2}} \:\:\mathrm{8}×\:\frac{{t}−\mathrm{2}}{\mathrm{64}−\left({t}^{\mathrm{3}} −\mathrm{4}\right)^{\mathrm{3}} } \\ $$$$={lim}_{{t}\rightarrow\mathrm{2}} \:\:\:\frac{\mathrm{8}\left({t}−\mathrm{2}\right)}{\mathrm{64}−\left({t}^{\mathrm{9}} \:−\mathrm{3}{t}^{\mathrm{6}} \left(\mathrm{4}\right)+\mathrm{3}{t}^{\mathrm{3}} \mathrm{4}^{\mathrm{2}} −\mathrm{4}^{\mathrm{3}} \right)} \\ $$$$={lim}_{{t}\rightarrow\mathrm{2}} \:\:\:\frac{\mathrm{8}\left({t}−\mathrm{2}\right)}{\mathrm{64}−{t}^{\mathrm{9}} +\mathrm{12}{t}^{\mathrm{6}} −\mathrm{48}{t}^{\mathrm{3}} \:+\mathrm{64}}\:={lim}_{{t}\rightarrow\mathrm{2}} \:\frac{\mathrm{8}\left({t}−\mathrm{2}\right)}{−{t}^{\mathrm{9}} \:+\mathrm{12}{t}^{\mathrm{6}} −\mathrm{48}{t}^{\mathrm{3}} \:+\mathrm{128}} \\ $$$$=_{{hop}} \:\:\:\:{lim}_{{t}\rightarrow\mathrm{2}} \:\:\:\frac{\mathrm{8}}{−\mathrm{9}{t}^{\mathrm{8}} \:+\mathrm{12}×\mathrm{6}{t}^{\mathrm{5}} \:−\mathrm{48}×\mathrm{3}\:{t}^{\mathrm{2}} }\:=\frac{\mathrm{8}}{−\mathrm{9}.\mathrm{2}^{\mathrm{8}} \:+\mathrm{12}×\mathrm{6}.\:\mathrm{2}^{\mathrm{5}} −\mathrm{48}.\mathrm{3}.\mathrm{2}^{\mathrm{2}} } \\ $$$$=….. \\ $$

Commented by hmamarques1994@gmail.com last updated on 18/Aug/19