Menu Close

lim-x-4-2x-2-16-4-4x-2-16x-1-2x-2-16-4-

Tinku Tara
Pin




Question Number 131388 by Eric002 last updated on 04/Feb/21
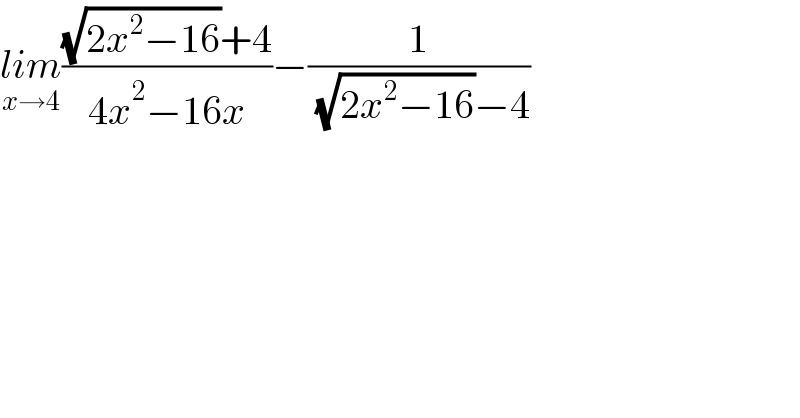
lim_(x→4) (((√(2x^2 −16))+4)/(4x^2 −16x))−(1/( (√(2x^2 −16))−4))
$$\underset{{x}\rightarrow\mathrm{4}} {{lim}}\frac{\sqrt{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{16}}+\mathrm{4}}{\mathrm{4}{x}^{\mathrm{2}} −\mathrm{16}{x}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{16}}−\mathrm{4}} \\ $$
Answered by bemath last updated on 04/Feb/21
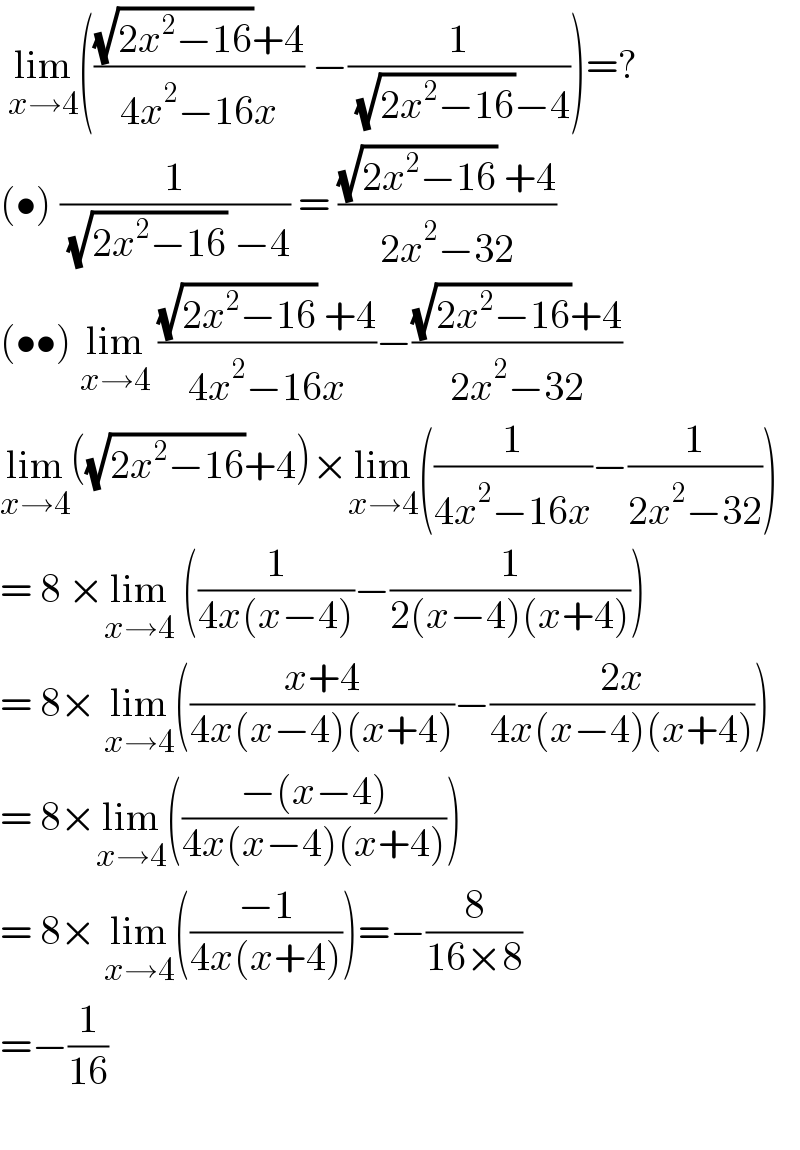
lim_(x→4) ((((√(2x^2 −16))+4)/(4x^2 −16x)) −(1/( (√(2x^2 −16))−4)))=? (•) (1/( (√(2x^2 −16)) −4)) = (((√(2x^2 −16)) +4)/(2x^2 −32)) (••) lim_(x→4) (((√(2x^2 −16)) +4)/(4x^2 −16x))−(((√(2x^2 −16))+4)/(2x^2 −32)) lim_(x→4) ((√(2x^2 −16))+4)×lim_(x→4) ((1/(4x^2 −16x))−(1/(2x^2 −32))) = 8 ×lim_(x→4) ((1/(4x(x−4)))−(1/(2(x−4)(x+4)))) = 8× lim_(x→4) (((x+4)/(4x(x−4)(x+4)))−((2x)/(4x(x−4)(x+4)))) = 8×lim_(x→4) (((−(x−4))/(4x(x−4)(x+4)))) = 8× lim_(x→4) (((−1)/(4x(x+4))))=−(8/(16×8)) =−(1/(16))
$$\:\underset{{x}\rightarrow\mathrm{4}} {\mathrm{lim}}\left(\frac{\sqrt{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{16}}+\mathrm{4}}{\mathrm{4}{x}^{\mathrm{2}} −\mathrm{16}{x}}\:−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{16}}−\mathrm{4}}\right)=? \\ $$$$\left(\bullet\right)\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{16}}\:−\mathrm{4}}\:=\:\frac{\sqrt{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{16}}\:+\mathrm{4}}{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{32}} \\ $$$$\left(\bullet\bullet\right)\:\underset{{x}\rightarrow\mathrm{4}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{16}}\:+\mathrm{4}}{\mathrm{4}{x}^{\mathrm{2}} −\mathrm{16}{x}}−\frac{\sqrt{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{16}}+\mathrm{4}}{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{32}} \\ $$$$\underset{{x}\rightarrow\mathrm{4}} {\mathrm{lim}}\left(\sqrt{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{16}}+\mathrm{4}\right)×\underset{{x}\rightarrow\mathrm{4}} {\mathrm{lim}}\left(\frac{\mathrm{1}}{\mathrm{4}{x}^{\mathrm{2}} −\mathrm{16}{x}}−\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{32}}\right) \\ $$$$=\:\mathrm{8}\:×\underset{{x}\rightarrow\mathrm{4}} {\mathrm{lim}}\:\left(\frac{\mathrm{1}}{\mathrm{4}{x}\left({x}−\mathrm{4}\right)}−\frac{\mathrm{1}}{\mathrm{2}\left({x}−\mathrm{4}\right)\left({x}+\mathrm{4}\right)}\right) \\ $$$$=\:\mathrm{8}×\:\underset{{x}\rightarrow\mathrm{4}} {\mathrm{lim}}\left(\frac{{x}+\mathrm{4}}{\mathrm{4}{x}\left({x}−\mathrm{4}\right)\left({x}+\mathrm{4}\right)}−\frac{\mathrm{2}{x}}{\mathrm{4}{x}\left({x}−\mathrm{4}\right)\left({x}+\mathrm{4}\right)}\right) \\ $$$$=\:\mathrm{8}×\underset{{x}\rightarrow\mathrm{4}} {\mathrm{lim}}\left(\frac{−\left({x}−\mathrm{4}\right)}{\mathrm{4}{x}\left({x}−\mathrm{4}\right)\left({x}+\mathrm{4}\right)}\right) \\ $$$$=\:\mathrm{8}×\:\underset{{x}\rightarrow\mathrm{4}} {\mathrm{lim}}\left(\frac{−\mathrm{1}}{\mathrm{4}{x}\left({x}+\mathrm{4}\right)}\right)=−\frac{\mathrm{8}}{\mathrm{16}×\mathrm{8}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{16}} \\ $$$$\:\:\:\:\:\: \\ $$
Commented by bramlexs22 last updated on 04/Feb/21
Wow es ist so cool Sir
$$ \\ $$$$\mathrm{Wow}\:\mathrm{es}\:\mathrm{ist}\:\mathrm{so}\:\mathrm{cool}\:\mathrm{Sir} \\ $$
Commented by Eric002 last updated on 04/Feb/21
well done sir
$${well}\:{done}\:{sir} \\ $$

Pin