lim-x-8-x-1-3-2-x-2-2-

Question Number 134173 by mathlove last updated on 28/Feb/21

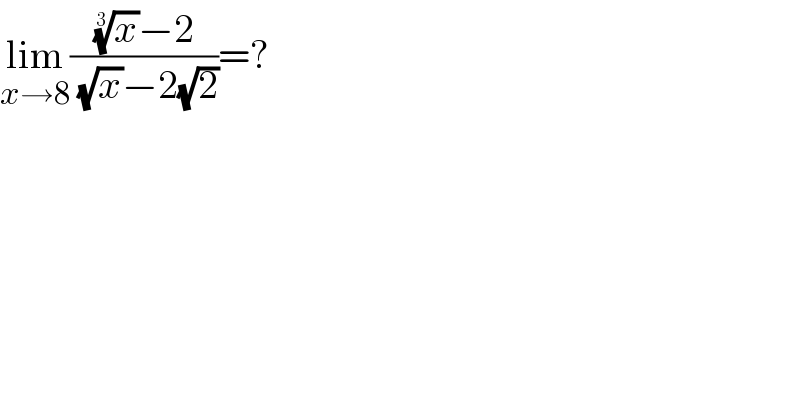
$$\underset{{x}\rightarrow\mathrm{8}} {\mathrm{lim}}\frac{\sqrt[{\mathrm{3}}]{{x}}−\mathrm{2}}{\:\sqrt{{x}}−\mathrm{2}\sqrt{\mathrm{2}}}=? \\ $$

Answered by malwan last updated on 28/Feb/21

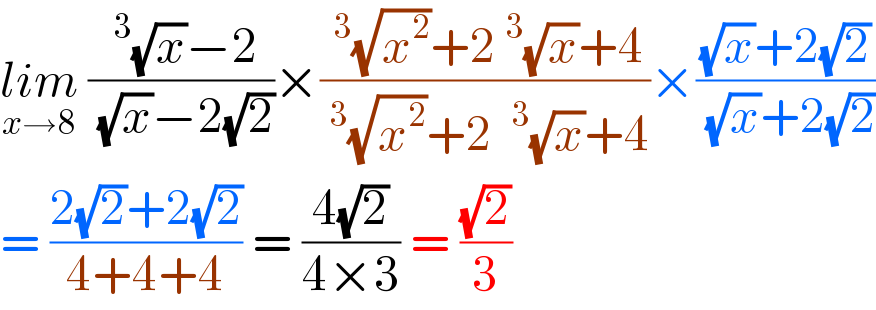
lim_(x→8) ((^3 (√x)−2)/( (√x)−2(√2)))×((^3 (√x^2 )+2^3 (√x)+4)/(^3 (√x^2 )+2 ^3 (√x)+4))×(((√x)+2(√2))/( (√x)+2(√2))) = ((2(√2)+2(√2))/(4+4+4)) = ((4(√2))/(4×3)) = ((√2)/3)

$$\underset{{x}\rightarrow\mathrm{8}} {{lim}}\:\frac{\:^{\mathrm{3}} \sqrt{{x}}−\mathrm{2}}{\:\sqrt{{x}}−\mathrm{2}\sqrt{\mathrm{2}}}×\frac{\:^{\mathrm{3}} \sqrt{{x}^{\mathrm{2}} }+\mathrm{2}\:^{\mathrm{3}} \sqrt{{x}}+\mathrm{4}}{\:^{\mathrm{3}} \sqrt{{x}^{\mathrm{2}} }+\mathrm{2}\:\:^{\mathrm{3}} \sqrt{{x}}+\mathrm{4}}×\frac{\sqrt{{x}}+\mathrm{2}\sqrt{\mathrm{2}}}{\:\sqrt{{x}}+\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$=\:\frac{\mathrm{2}\sqrt{\mathrm{2}}+\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{4}+\mathrm{4}+\mathrm{4}}\:=\:\frac{\mathrm{4}\sqrt{\mathrm{2}}}{\mathrm{4}×\mathrm{3}}\:=\:\frac{\sqrt{\mathrm{2}}}{\mathrm{3}} \\ $$

Answered by EDWIN88 last updated on 02/Mar/21

let x = t^6 ⇒lim_(t→(√2)) [ ((t^2 −2)/(t^3 −2(√2))) ] = lim_(t→(√2)) ((2t)/(3t^2 )) = (2/(3×(√2))) = ((√2)/3)

$$\mathrm{let}\:\mathrm{x}\:=\:\mathrm{t}^{\mathrm{6}} \:\Rightarrow\underset{\mathrm{t}\rightarrow\sqrt{\mathrm{2}}} {\mathrm{lim}}\:\:\:\left[\:\frac{\mathrm{t}^{\mathrm{2}} −\mathrm{2}}{\mathrm{t}^{\mathrm{3}} −\mathrm{2}\sqrt{\mathrm{2}}}\:\right]\:=\:\underset{\mathrm{t}\rightarrow\sqrt{\mathrm{2}}} {\mathrm{lim}}\:\:\:\frac{\mathrm{2t}}{\mathrm{3t}^{\mathrm{2}} }\:=\:\frac{\mathrm{2}}{\mathrm{3}×\sqrt{\mathrm{2}}} \\ $$$$\:=\:\frac{\sqrt{\mathrm{2}}}{\mathrm{3}} \\ $$

Commented by malwan last updated on 02/Mar/21

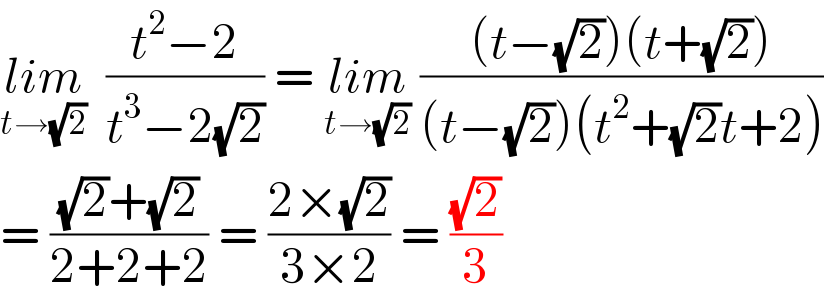
lim_(t→(√2)) ((t^2 −2)/(t^3 −2(√2))) = lim_(t→(√2)) (((t−(√2))(t+(√2)))/((t−(√2))(t^2 +(√2)t+2))) = (((√2)+(√2))/(2+2+2)) = ((2×(√2))/(3×2)) = ((√2)/3)

$$\underset{{t}\rightarrow\sqrt{\mathrm{2}}} {{lim}}\:\:\frac{{t}^{\mathrm{2}} −\mathrm{2}}{{t}^{\mathrm{3}} −\mathrm{2}\sqrt{\mathrm{2}}}\:=\:\underset{{t}\rightarrow\sqrt{\mathrm{2}}} {{lim}}\:\frac{\left({t}−\sqrt{\mathrm{2}}\right)\left({t}+\sqrt{\mathrm{2}}\right)}{\left({t}−\sqrt{\mathrm{2}}\right)\left({t}^{\mathrm{2}} +\sqrt{\mathrm{2}}{t}+\mathrm{2}\right)} \\ $$$$=\:\frac{\sqrt{\mathrm{2}}+\sqrt{\mathrm{2}}}{\mathrm{2}+\mathrm{2}+\mathrm{2}}\:=\:\frac{\mathrm{2}×\sqrt{\mathrm{2}}}{\mathrm{3}×\mathrm{2}}\:=\:\frac{\sqrt{\mathrm{2}}}{\mathrm{3}} \\ $$

Facebook Tweet Pin

lim-x-8-x-1-3-2-x-2-2-

Leave a Reply Cancel reply