Question Number 142444 by mathdanisur last updated on 31/May/21
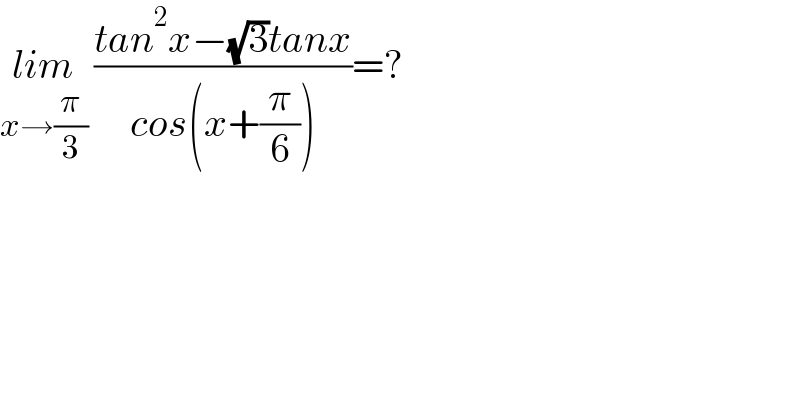
$$\underset{{x}\rightarrow\frac{\pi}{\mathrm{3}}} {{lim}}\:\frac{{tan}^{\mathrm{2}} {x}−\sqrt{\mathrm{3}}{tanx}}{{cos}\left({x}+\frac{\pi}{\mathrm{6}}\right)}=? \\ $$
Answered by bramlexs22 last updated on 31/May/21
![lim_(x→(π/3)) ((tan^2 x−(√3) tan x)/(cos (x+(π/6)))) =? set x = (π/3)+z and z→0 ⇔ lim_(z→0) ((tan (z+(π/3))[tan (z+(π/3))−(√(3 ))])/(cos (z+(π/2)))) = −lim_(z→0) tan (z+(π/3)).lim_(z→0) ((tan (z+(π/3))−(√3))/(sin z)) =−(√3) .lim_(z→0) ((sec^2 (z+(π/3)))/(cos z)) =−(√3) .lim_(z→0) (1/(cos^2 (z+(π/3)).cos z)) =−(√3) . (1/(((1/4)).1))=−4(√3)](https://www.tinkutara.com/question/Q142453.png)
$$\:\underset{{x}\rightarrow\frac{\pi}{\mathrm{3}}} {\mathrm{lim}}\:\frac{\mathrm{tan}\:^{\mathrm{2}} {x}−\sqrt{\mathrm{3}}\:\mathrm{tan}\:{x}}{\mathrm{cos}\:\left({x}+\frac{\pi}{\mathrm{6}}\right)}\:=? \\ $$$$\:{set}\:{x}\:=\:\frac{\pi}{\mathrm{3}}+{z}\:{and}\:{z}\rightarrow\mathrm{0} \\ $$$$\Leftrightarrow\:\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{tan}\:\left({z}+\frac{\pi}{\mathrm{3}}\right)\left[\mathrm{tan}\:\left({z}+\frac{\pi}{\mathrm{3}}\right)−\sqrt{\mathrm{3}\:}\right]}{\mathrm{cos}\:\left({z}+\frac{\pi}{\mathrm{2}}\right)} \\ $$$$=\:−\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{tan}\:\left({z}+\frac{\pi}{\mathrm{3}}\right).\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{tan}\:\left({z}+\frac{\pi}{\mathrm{3}}\right)−\sqrt{\mathrm{3}}}{\mathrm{sin}\:{z}} \\ $$$$=−\sqrt{\mathrm{3}}\:.\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sec}\:^{\mathrm{2}} \left({z}+\frac{\pi}{\mathrm{3}}\right)}{\mathrm{cos}\:{z}} \\ $$$$=−\sqrt{\mathrm{3}}\:.\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{cos}\:^{\mathrm{2}} \left({z}+\frac{\pi}{\mathrm{3}}\right).\mathrm{cos}\:{z}} \\ $$$$=−\sqrt{\mathrm{3}}\:.\:\frac{\mathrm{1}}{\left(\frac{\mathrm{1}}{\mathrm{4}}\right).\mathrm{1}}=−\mathrm{4}\sqrt{\mathrm{3}} \\ $$
Commented by mathdanisur last updated on 02/Jun/21

$${thankyou}\:{sir} \\ $$
