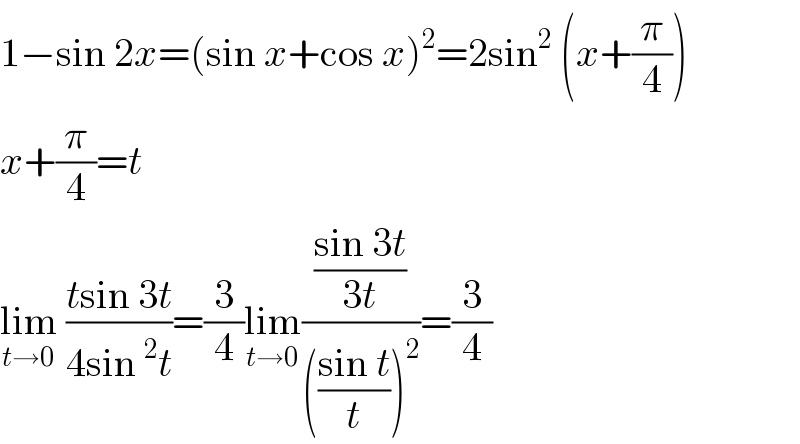Menu Close

lim-x-pi-4-x-pi-4-sin-3x-3-pi-4-2-1-sin2x-

Tinku Tara 0 Comments
Pin




Question Number 10374 by ridwan balatif last updated on 06/Feb/17
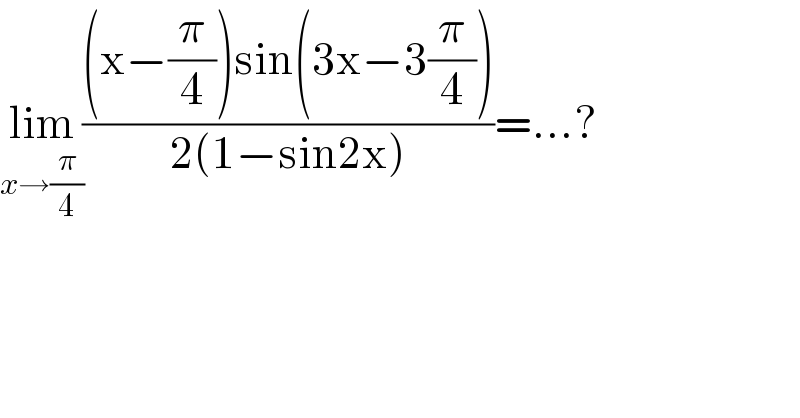
lim_(x→(π/4)) (((x−(π/4))sin(3x−3(π/4)))/(2(1−sin2x)))=...?
$$\underset{{x}\rightarrow\frac{\pi}{\mathrm{4}}} {\mathrm{lim}}\frac{\left(\mathrm{x}−\frac{\pi}{\mathrm{4}}\right)\mathrm{sin}\left(\mathrm{3x}−\mathrm{3}\frac{\pi}{\mathrm{4}}\right)}{\mathrm{2}\left(\mathrm{1}−\mathrm{sin2x}\right)}=…? \\ $$
Answered by mrW1 last updated on 06/Feb/17
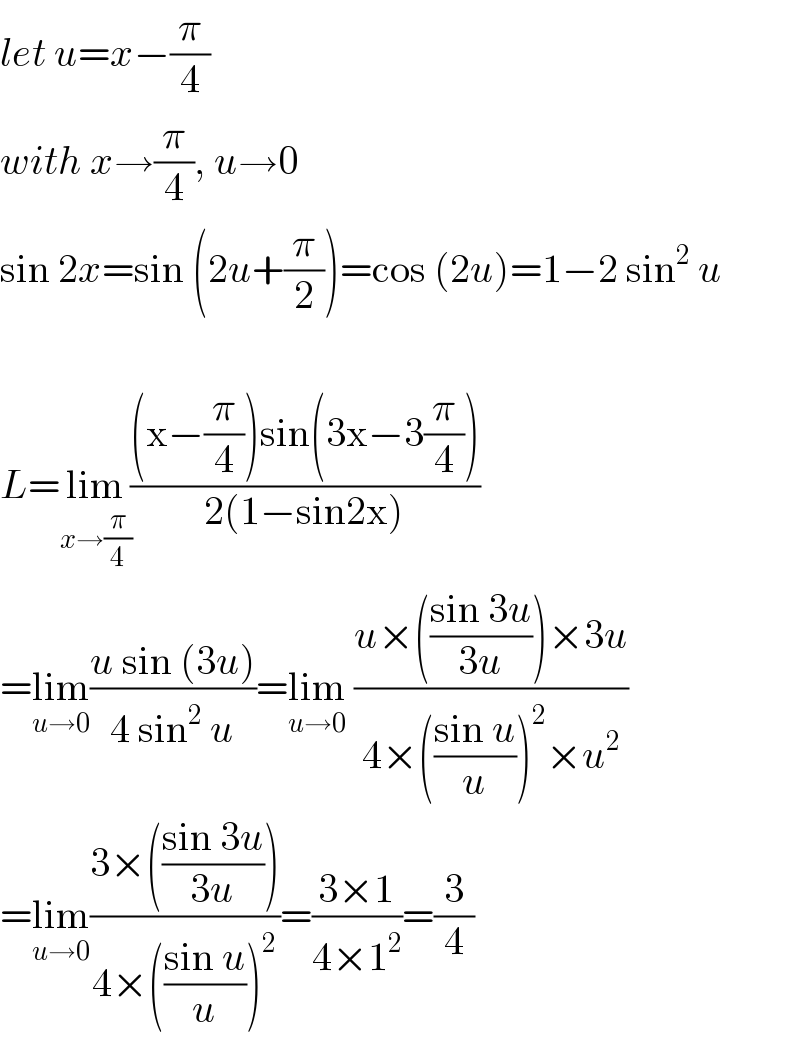
let u=x−(π/4) with x→(π/4), u→0 sin 2x=sin (2u+(π/2))=cos (2u)=1−2 sin^2 u L=lim_(x→(π/4)) (((x−(π/4))sin(3x−3(π/4)))/(2(1−sin2x))) =lim_(u→0) ((u sin (3u))/(4 sin^2 u))=lim_(u→0) ((u×(((sin 3u)/(3u)))×3u)/(4×(((sin u)/u))^2 ×u^2 )) =lim_(u→0) ((3×(((sin 3u)/(3u))))/(4×(((sin u)/u))^2 ))=((3×1)/(4×1^2 ))=(3/4)
$${let}\:{u}={x}−\frac{\pi}{\mathrm{4}} \\ $$$${with}\:{x}\rightarrow\frac{\pi}{\mathrm{4}},\:{u}\rightarrow\mathrm{0} \\ $$$$\mathrm{sin}\:\mathrm{2}{x}=\mathrm{sin}\:\left(\mathrm{2}{u}+\frac{\pi}{\mathrm{2}}\right)=\mathrm{cos}\:\left(\mathrm{2}{u}\right)=\mathrm{1}−\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:{u} \\ $$$$ \\ $$$${L}=\underset{{x}\rightarrow\frac{\pi}{\mathrm{4}}} {\mathrm{lim}}\frac{\left(\mathrm{x}−\frac{\pi}{\mathrm{4}}\right)\mathrm{sin}\left(\mathrm{3x}−\mathrm{3}\frac{\pi}{\mathrm{4}}\right)}{\mathrm{2}\left(\mathrm{1}−\mathrm{sin2x}\right)} \\ $$$$=\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{u}\:\mathrm{sin}\:\left(\mathrm{3}{u}\right)}{\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:{u}}=\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{u}×\left(\frac{\mathrm{sin}\:\mathrm{3}{u}}{\mathrm{3}{u}}\right)×\mathrm{3}{u}}{\mathrm{4}×\left(\frac{\mathrm{sin}\:{u}}{{u}}\right)^{\mathrm{2}} ×{u}^{\mathrm{2}} } \\ $$$$=\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{3}×\left(\frac{\mathrm{sin}\:\mathrm{3}{u}}{\mathrm{3}{u}}\right)}{\mathrm{4}×\left(\frac{\mathrm{sin}\:{u}}{{u}}\right)^{\mathrm{2}} }=\frac{\mathrm{3}×\mathrm{1}}{\mathrm{4}×\mathrm{1}^{\mathrm{2}} }=\frac{\mathrm{3}}{\mathrm{4}} \\ $$
Commented by ridwan balatif last updated on 06/Feb/17
thank you sir
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by arge last updated on 08/Feb/17
por l′hopital, y=(((x−(x/4))sen(3x−((12+π)/4)))/(2(1−sen2x))) y′=((2(1−sen2x)[(x−(x/4))cos(3x−((12+π)/4))+sen(3x−((12+π)/4))(1−(1/4))]−(x−(x/4))sen(3x−((12+π)/4))×2(−cos2x))/(4(1−2sen2x+4sen^2 xcos^2 x))) y′=(A/0) A=_ −134.65, y′=∞∵∵∵∵∵Rta
$${por}\:{l}'{hopital}, \\ $$$$ \\ $$$${y}=\frac{\left({x}−\frac{{x}}{\mathrm{4}}\right){sen}\left(\mathrm{3}{x}−\frac{\mathrm{12}+\pi}{\mathrm{4}}\right)}{\mathrm{2}\left(\mathrm{1}−{sen}\mathrm{2}{x}\right)} \\ $$$$ \\ $$$${y}'=\frac{\mathrm{2}\left(\mathrm{1}−{sen}\mathrm{2}{x}\right)\left[\left({x}−\frac{{x}}{\mathrm{4}}\right){cos}\left(\mathrm{3}{x}−\frac{\mathrm{12}+\pi}{\mathrm{4}}\right)+{sen}\left(\mathrm{3}{x}−\frac{\mathrm{12}+\pi}{\mathrm{4}}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}\right)\right]−\left({x}−\frac{{x}}{\mathrm{4}}\right){sen}\left(\mathrm{3}{x}−\frac{\mathrm{12}+\pi}{\mathrm{4}}\right)×\mathrm{2}\left(−{cos}\mathrm{2}{x}\right)}{\mathrm{4}\left(\mathrm{1}−\mathrm{2}{sen}\mathrm{2}{x}+\mathrm{4}{sen}^{\mathrm{2}} {xcos}^{\mathrm{2}} {x}\right)} \\ $$$$ \\ $$$${y}'=\frac{{A}}{\mathrm{0}} \\ $$$$ \\ $$$${A}\underset{} {=}\:\:−\mathrm{134}.\mathrm{65},\:{y}'=\infty\because\because\because\because\because{Rta} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Answered by bahmanfeshki last updated on 02/Mar/17
1−sin 2x=(sin x+cos x)^2 =2sin^2 (x+(π/4)) x+(π/4)=t lim_(t→0) ((tsin 3t)/(4sin^2 t))=(3/4)lim_(t→0) (((sin 3t)/(3t))/((((sin t)/t))^2 ))=(3/4)
$$\mathrm{1}−\mathrm{sin}\:\mathrm{2}{x}=\left(\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\right)^{\mathrm{2}} =\mathrm{2sin}^{\mathrm{2}} \:\left({x}+\frac{\pi}{\mathrm{4}}\right) \\ $$$${x}+\frac{\pi}{\mathrm{4}}={t} \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{t}\mathrm{sin}\:\mathrm{3}{t}}{\mathrm{4sin}\:^{\mathrm{2}} {t}}=\frac{\mathrm{3}}{\mathrm{4}}\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{sin}\:\mathrm{3}{t}}{\mathrm{3}{t}}}{\left(\frac{\mathrm{sin}\:{t}}{{t}}\right)^{\mathrm{2}} }=\frac{\mathrm{3}}{\mathrm{4}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *