Question Number 142151 by iloveisrael last updated on 27/May/21

$$\:\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{sin}\:\sqrt{{x}+\mathrm{1}}−\mathrm{sin}\:\sqrt{{x}}\:=? \\ $$
Commented by gsk2684 last updated on 27/May/21
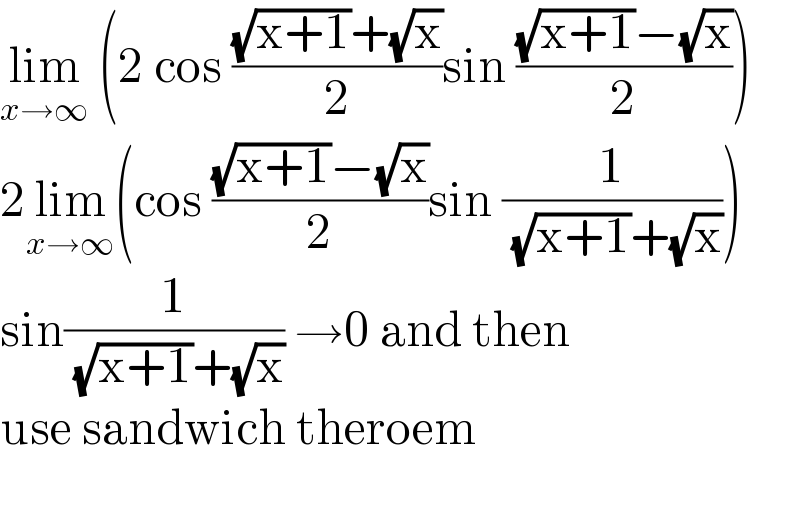
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\mathrm{2}\:\mathrm{cos}\:\frac{\sqrt{\mathrm{x}+\mathrm{1}}+\sqrt{\mathrm{x}}}{\mathrm{2}}\mathrm{sin}\:\frac{\sqrt{\mathrm{x}+\mathrm{1}}−\sqrt{\mathrm{x}}}{\mathrm{2}}\right) \\ $$$$\mathrm{2}\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{cos}\:\frac{\sqrt{\mathrm{x}+\mathrm{1}}−\sqrt{\mathrm{x}}}{\mathrm{2}}\mathrm{sin}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{x}+\mathrm{1}}+\sqrt{\mathrm{x}}}\right) \\ $$$$\mathrm{sin}\frac{\mathrm{1}}{\:\sqrt{\mathrm{x}+\mathrm{1}}+\sqrt{\mathrm{x}}}\:\rightarrow\mathrm{0}\:\mathrm{and}\:\mathrm{then} \\ $$$$\mathrm{use}\:\mathrm{sandwich}\:\mathrm{theroem} \\ $$$$ \\ $$
