Question Number 141356 by physicstutes last updated on 17/May/21
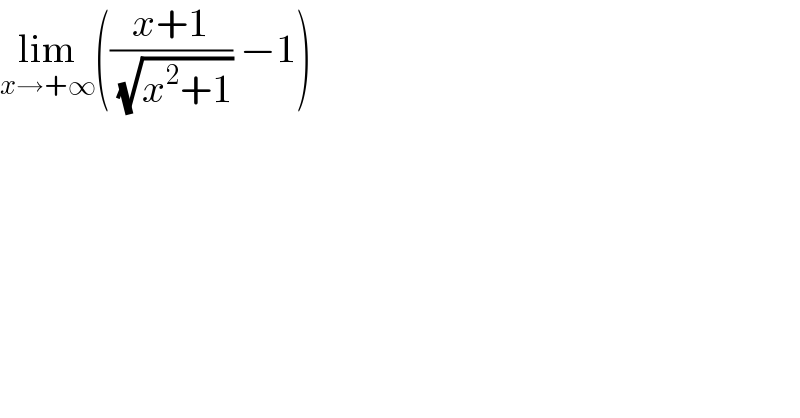
$$\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\left(\frac{{x}+\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}\:−\mathrm{1}\right) \\ $$
Answered by bemath last updated on 18/May/21
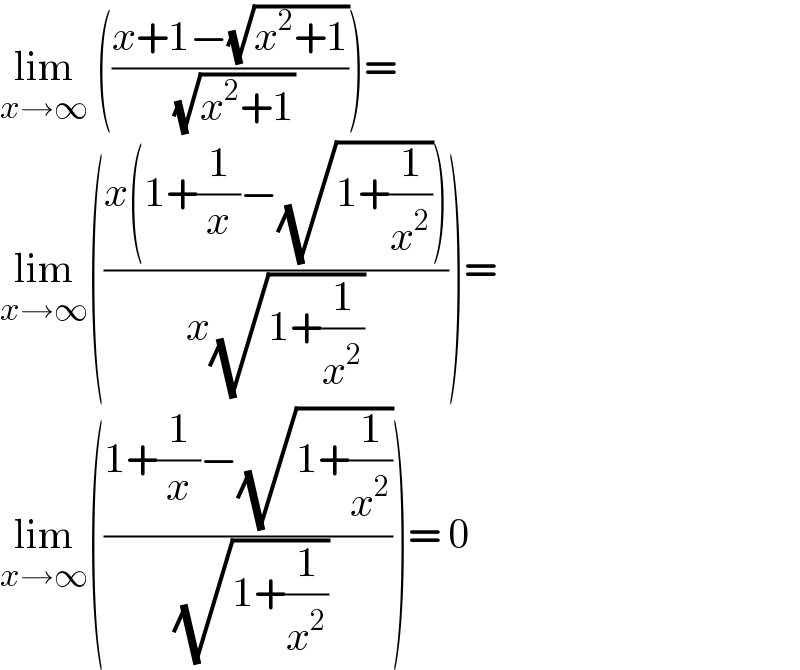
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\frac{{x}+\mathrm{1}−\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}\right)= \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{{x}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}−\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}\right)}{{x}\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}}\right)= \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{1}+\frac{\mathrm{1}}{{x}}−\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}}{\:\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}}\right)=\:\mathrm{0}\: \\ $$
Answered by Mathspace last updated on 18/May/21
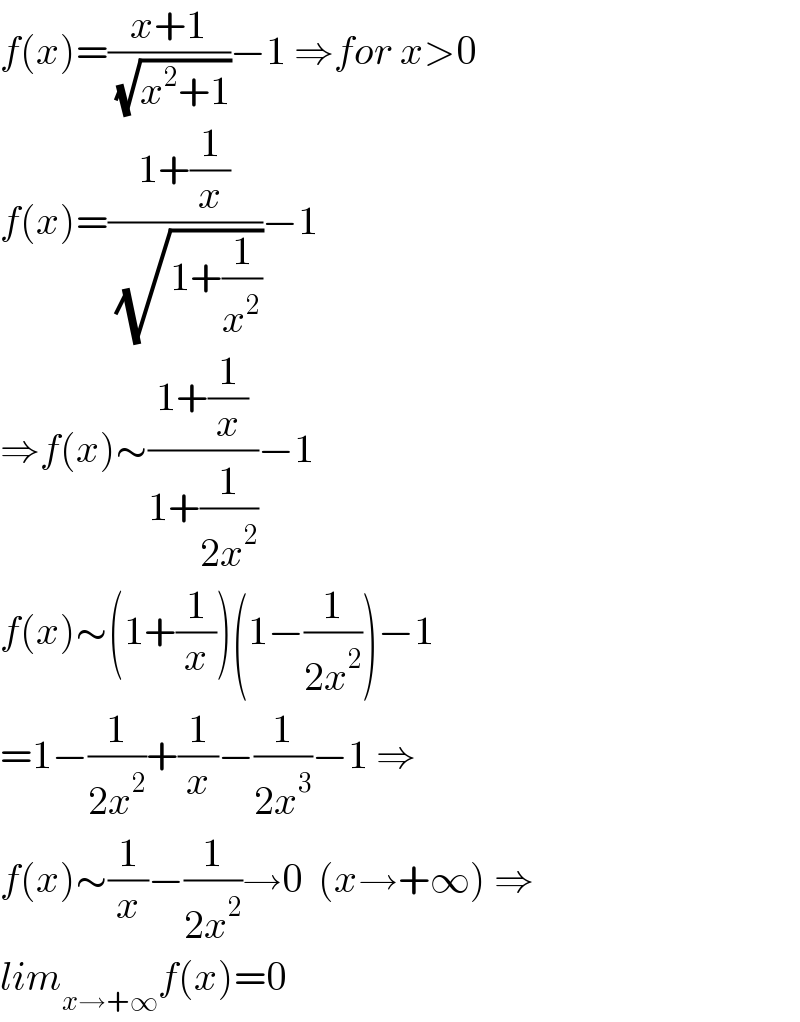
$${f}\left({x}\right)=\frac{{x}+\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}−\mathrm{1}\:\Rightarrow{for}\:{x}>\mathrm{0} \\ $$$${f}\left({x}\right)=\frac{\mathrm{1}+\frac{\mathrm{1}}{{x}}}{\:\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}}−\mathrm{1} \\ $$$$\Rightarrow{f}\left({x}\right)\sim\frac{\mathrm{1}+\frac{\mathrm{1}}{{x}}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }}−\mathrm{1} \\ $$$${f}\left({x}\right)\sim\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }\right)−\mathrm{1} \\ $$$$=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{3}} }−\mathrm{1}\:\Rightarrow \\ $$$${f}\left({x}\right)\sim\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }\rightarrow\mathrm{0}\:\:\left({x}\rightarrow+\infty\right)\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow+\infty} {f}\left({x}\right)=\mathrm{0} \\ $$
