Question Number 131156 by EDWIN88 last updated on 02/Feb/21
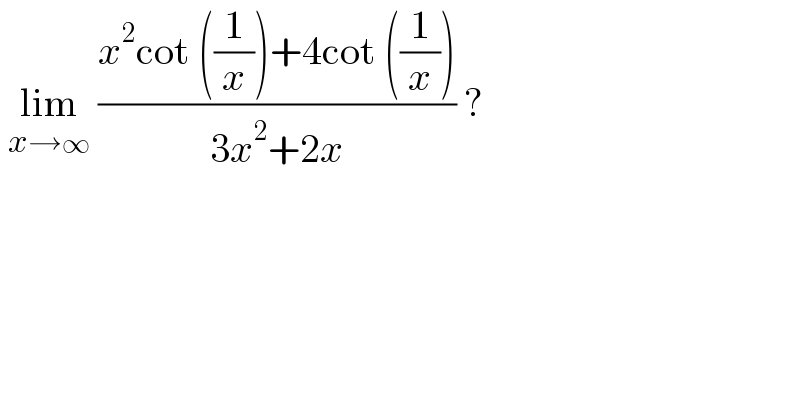
$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{{x}^{\mathrm{2}} \mathrm{cot}\:\left(\frac{\mathrm{1}}{{x}}\right)+\mathrm{4cot}\:\left(\frac{\mathrm{1}}{{x}}\right)}{\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}{x}}\:? \\ $$
Answered by john_santu last updated on 02/Feb/21
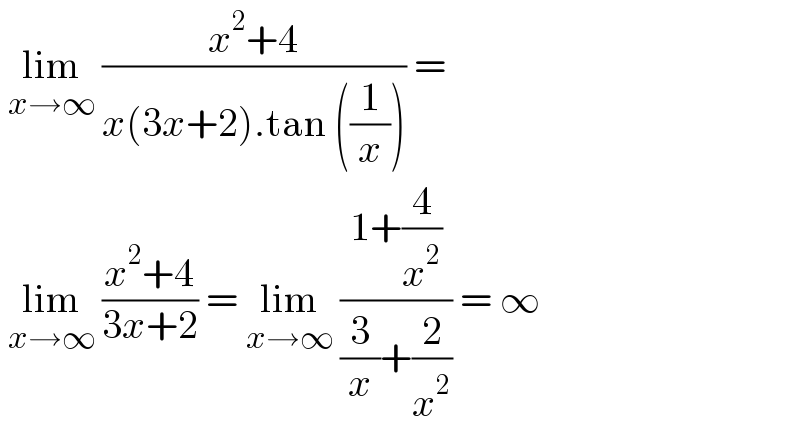
$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{{x}^{\mathrm{2}} +\mathrm{4}}{{x}\left(\mathrm{3}{x}+\mathrm{2}\right).\mathrm{tan}\:\left(\frac{\mathrm{1}}{{x}}\right)}\:=\: \\ $$$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{{x}^{\mathrm{2}} +\mathrm{4}}{\mathrm{3}{x}+\mathrm{2}}\:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}+\frac{\mathrm{4}}{{x}^{\mathrm{2}} }}{\frac{\mathrm{3}}{{x}}+\frac{\mathrm{2}}{{x}^{\mathrm{2}} }}\:=\:\infty \\ $$
