Question Number 133758 by EDWIN88 last updated on 24/Feb/21
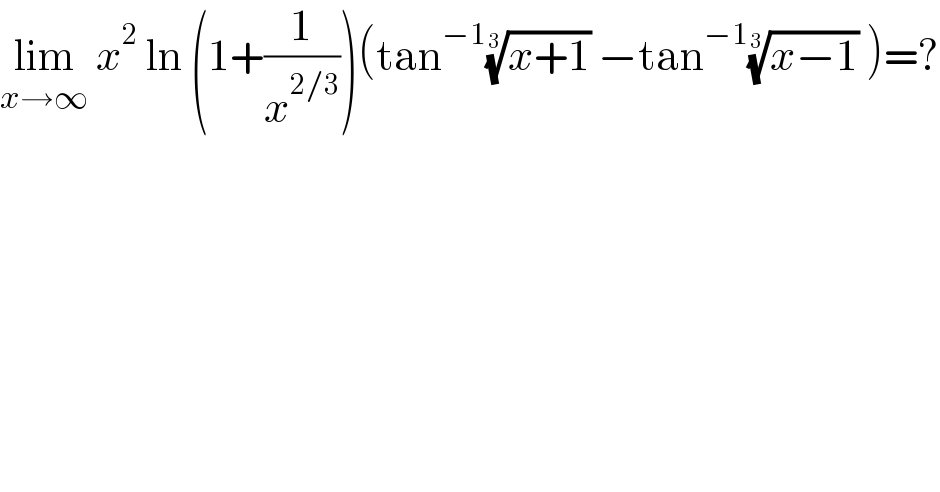
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{x}^{\mathrm{2}} \:\mathrm{ln}\:\left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}/\mathrm{3}} }\right)\left(\mathrm{tan}^{−\mathrm{1}} \sqrt[{\mathrm{3}}]{{x}+\mathrm{1}}\:−\mathrm{tan}^{−\mathrm{1}} \sqrt[{\mathrm{3}}]{{x}−\mathrm{1}}\:\right)=? \\ $$
Answered by liberty last updated on 24/Feb/21
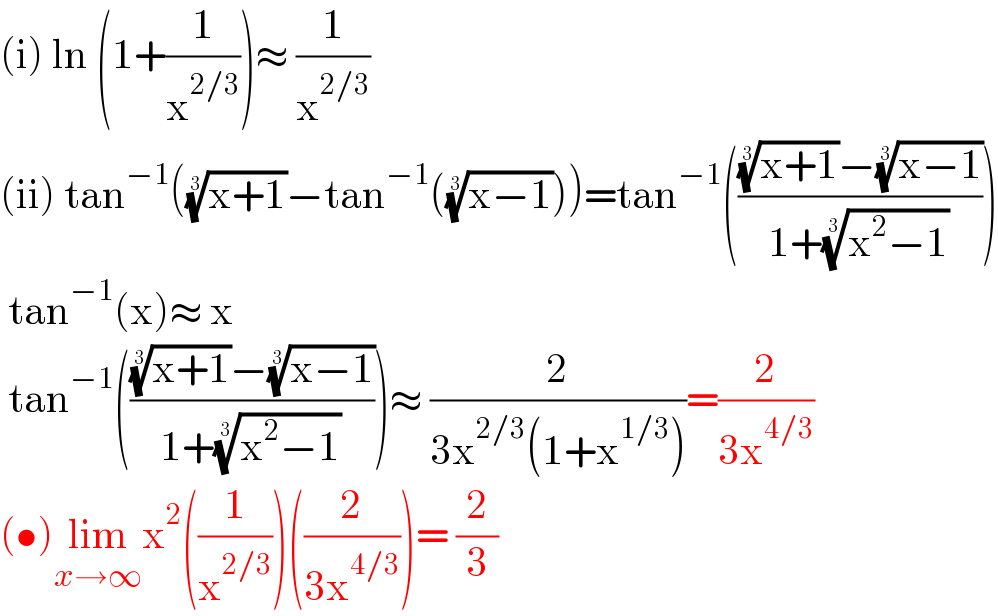
$$\left(\mathrm{i}\right)\:\mathrm{ln}\:\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}/\mathrm{3}} }\right)\approx\:\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}/\mathrm{3}} } \\ $$$$\left(\mathrm{ii}\right)\:\mathrm{tan}^{−\mathrm{1}} \left(\sqrt[{\mathrm{3}}]{\mathrm{x}+\mathrm{1}}−\mathrm{tan}^{−\mathrm{1}} \left(\sqrt[{\mathrm{3}}]{\mathrm{x}−\mathrm{1}}\right)\right)=\mathrm{tan}^{−\mathrm{1}} \left(\frac{\sqrt[{\mathrm{3}}]{\mathrm{x}+\mathrm{1}}−\sqrt[{\mathrm{3}}]{\mathrm{x}−\mathrm{1}}}{\mathrm{1}+\sqrt[{\mathrm{3}}]{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}}\right) \\ $$$$\:\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{x}\right)\approx\:\mathrm{x} \\ $$$$\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\sqrt[{\mathrm{3}}]{\mathrm{x}+\mathrm{1}}−\sqrt[{\mathrm{3}}]{\mathrm{x}−\mathrm{1}}}{\mathrm{1}+\sqrt[{\mathrm{3}}]{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}}\right)\approx\:\frac{\mathrm{2}}{\mathrm{3x}^{\mathrm{2}/\mathrm{3}} \left(\mathrm{1}+\mathrm{x}^{\mathrm{1}/\mathrm{3}} \right)}=\frac{\mathrm{2}}{\mathrm{3x}^{\mathrm{4}/\mathrm{3}} } \\ $$$$\left(\bullet\right)\underset{{x}\rightarrow\infty} {\mathrm{lim}x}^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}/\mathrm{3}} }\right)\left(\frac{\mathrm{2}}{\mathrm{3x}^{\mathrm{4}/\mathrm{3}} }\right)=\:\frac{\mathrm{2}}{\mathrm{3}} \\ $$
