Question Number 131386 by bemath last updated on 04/Feb/21
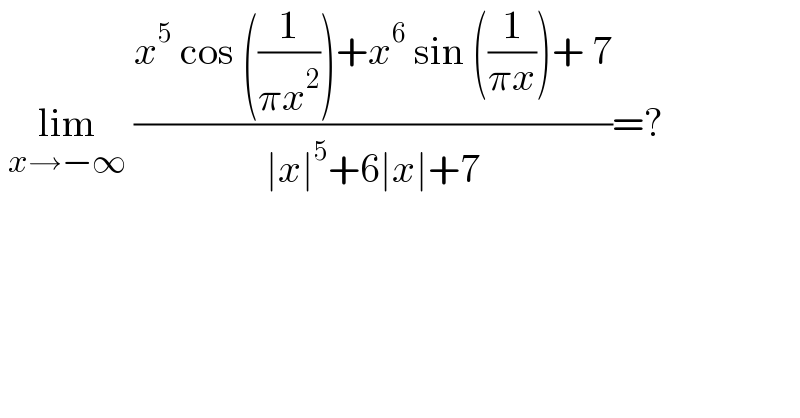
$$\:\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:\frac{{x}^{\mathrm{5}} \:\mathrm{cos}\:\left(\frac{\mathrm{1}}{\pi{x}^{\mathrm{2}} }\right)+{x}^{\mathrm{6}} \:\mathrm{sin}\:\left(\frac{\mathrm{1}}{\pi{x}}\right)+\:\mathrm{7}}{\mid{x}\mid^{\mathrm{5}} +\mathrm{6}\mid{x}\mid+\mathrm{7}}=? \\ $$
Answered by liberty last updated on 04/Feb/21
![lim_(x→−∞) ((x^5 cos ((1/(πx^2 )))+x^6 sin ((1/(πx)))+7)/(∣x∣^5 +6∣x∣+7))=? remark ∣x∣=−x as x→−∞ lim_(x→−∞) ((x^5 cos ((1/(πx^2 )))+x^6 sin ((1/(πx)))+7)/(−x^5 −6x+7)) = lim_(x→−∞) ((cos ((1/(πx^2 )))+x sin ((1/(πx)))+(7/x^5 ))/(−1−(6/x^4 )+(7/x^5 ))) [ note : lim_(x→∞) x sin ((1/x))=1 ] = lim_(x→−∞) ((cos ((1/(πx^2 )))+x sin ((1/(πx)))+(7/x^5 ))/(−1−(6/x^4 )+(7/x^5 ))) = −1−(1/π)](https://www.tinkutara.com/question/Q131398.png)
$$\:\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:\frac{\mathrm{x}^{\mathrm{5}} \:\mathrm{cos}\:\left(\frac{\mathrm{1}}{\pi\mathrm{x}^{\mathrm{2}} }\right)+\mathrm{x}^{\mathrm{6}} \:\mathrm{sin}\:\left(\frac{\mathrm{1}}{\pi\mathrm{x}}\right)+\mathrm{7}}{\mid\mathrm{x}\mid^{\mathrm{5}} +\mathrm{6}\mid\mathrm{x}\mid+\mathrm{7}}=? \\ $$$$\:\mathrm{remark}\:\mid\mathrm{x}\mid=−\mathrm{x}\:\mathrm{as}\:\mathrm{x}\rightarrow−\infty \\ $$$$\:\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:\frac{\mathrm{x}^{\mathrm{5}} \:\mathrm{cos}\:\left(\frac{\mathrm{1}}{\pi\mathrm{x}^{\mathrm{2}} }\right)+\mathrm{x}^{\mathrm{6}} \:\mathrm{sin}\:\left(\frac{\mathrm{1}}{\pi\mathrm{x}}\right)+\mathrm{7}}{−\mathrm{x}^{\mathrm{5}} −\mathrm{6x}+\mathrm{7}} \\ $$$$=\:\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:\frac{\mathrm{cos}\:\left(\frac{\mathrm{1}}{\pi\mathrm{x}^{\mathrm{2}} }\right)+\mathrm{x}\:\mathrm{sin}\:\left(\frac{\mathrm{1}}{\pi\mathrm{x}}\right)+\frac{\mathrm{7}}{\mathrm{x}^{\mathrm{5}} }}{−\mathrm{1}−\frac{\mathrm{6}}{\mathrm{x}^{\mathrm{4}} }+\frac{\mathrm{7}}{\mathrm{x}^{\mathrm{5}} }} \\ $$$$\:\left[\:\mathrm{note}\::\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{x}\:\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{x}}\right)=\mathrm{1}\:\right] \\ $$$$=\:\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:\frac{\mathrm{cos}\:\left(\frac{\mathrm{1}}{\pi\mathrm{x}^{\mathrm{2}} }\right)+\mathrm{x}\:\mathrm{sin}\:\left(\frac{\mathrm{1}}{\pi\mathrm{x}}\right)+\frac{\mathrm{7}}{\mathrm{x}^{\mathrm{5}} }}{−\mathrm{1}−\frac{\mathrm{6}}{\mathrm{x}^{\mathrm{4}} }+\frac{\mathrm{7}}{\mathrm{x}^{\mathrm{5}} }}\:=\:−\mathrm{1}−\frac{\mathrm{1}}{\pi} \\ $$
Commented by liberty last updated on 04/Feb/21

Commented by bramlexs22 last updated on 04/Feb/21

$$ \\ $$$$\mathrm{ruhig}\:\mathrm{und}\:\mathrm{khl} \\ $$
