lim-x-x-k-e-4x-k-gt-0-

Question Number 76151 by Rio Michael last updated on 24/Dec/19

\lim_{x \to \infty} x^{k} e^{- 4 x}, k > 0

Commented by kaivan.ahmadi last updated on 24/Dec/19

{l i m}_{x - \to \infty} \frac{x^{k}}{e^{4 x}} = 0

Commented by kaivan.ahmadi last updated on 24/Dec/19

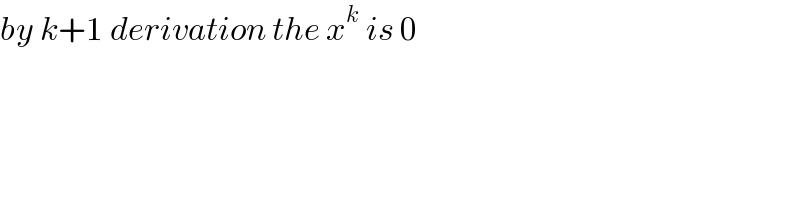
b y k + 1 d e r i v a t i o n t h e x^{k} i s 0

Commented by kaivan.ahmadi last updated on 24/Dec/19

{l i m}_{x \to \infty} \frac{0}{4^{k + 1} e^{4 x}} = 0

Commented by Rio Michael last updated on 24/Dec/19

t h a n k s

Commented by mr W last updated on 24/Dec/19

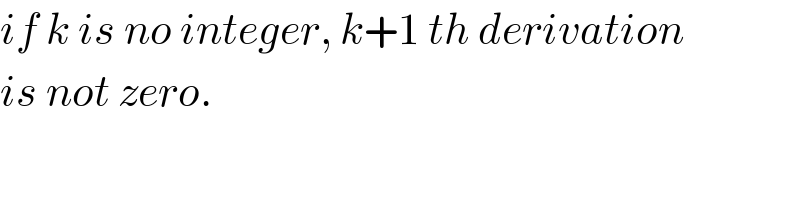
i f k i s n o i n t e g e r, k + 1 t h d e r i v a t i o n

i s n o t z e r o .

Commented by benjo last updated on 24/Dec/19

yes sir . i agree

Facebook Tweet Pin