Question Number 142329 by HarshSahu last updated on 30/May/21
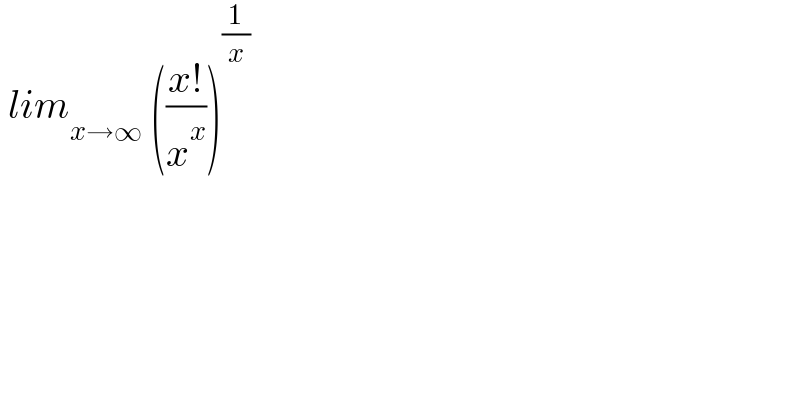
$$\:{lim}_{{x}\rightarrow\infty} \:\left(\frac{{x}!}{{x}^{{x}} }\right)^{\frac{\mathrm{1}}{{x}}} \\ $$
Answered by Dwaipayan Shikari last updated on 30/May/21
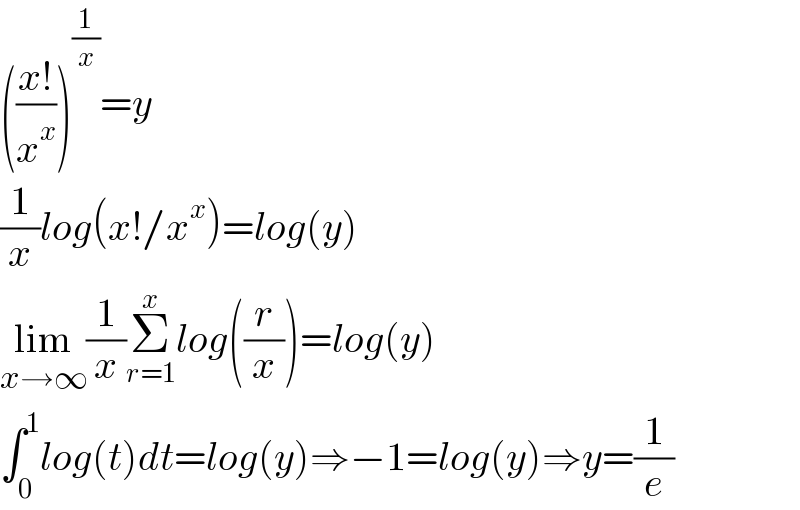
$$\left(\frac{{x}!}{{x}^{{x}} }\right)^{\frac{\mathrm{1}}{{x}}} ={y} \\ $$$$\frac{\mathrm{1}}{{x}}{log}\left({x}!/{x}^{{x}} \right)={log}\left({y}\right) \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{x}}\underset{{r}=\mathrm{1}} {\overset{{x}} {\sum}}{log}\left(\frac{{r}}{{x}}\right)={log}\left({y}\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {log}\left({t}\right){dt}={log}\left({y}\right)\Rightarrow−\mathrm{1}={log}\left({y}\right)\Rightarrow{y}=\frac{\mathrm{1}}{{e}} \\ $$
Answered by MJS_new last updated on 30/May/21
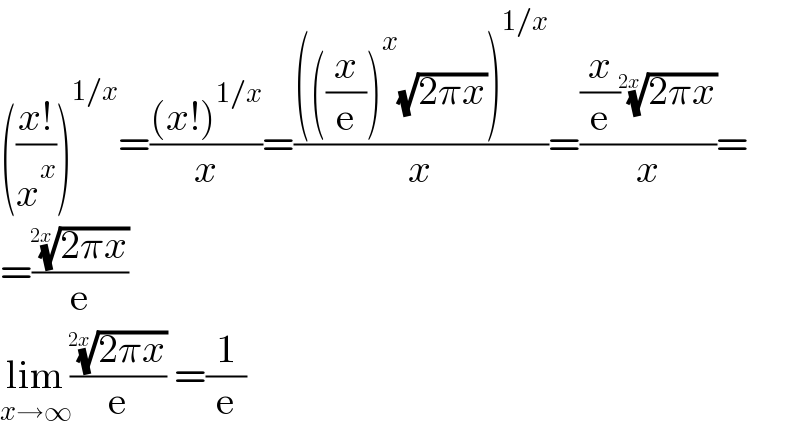
$$\left(\frac{{x}!}{{x}^{{x}} }\right)^{\mathrm{1}/{x}} =\frac{\left({x}!\right)^{\mathrm{1}/{x}} }{{x}}=\frac{\left(\left(\frac{{x}}{\mathrm{e}}\right)^{{x}} \sqrt{\mathrm{2}\pi{x}}\right)^{\mathrm{1}/{x}} }{{x}}=\frac{\frac{{x}}{\mathrm{e}}\sqrt[{\mathrm{2}{x}}]{\mathrm{2}\pi{x}}}{{x}}= \\ $$$$=\frac{\sqrt[{\mathrm{2}{x}}]{\mathrm{2}\pi{x}}}{\mathrm{e}} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\sqrt[{\mathrm{2}{x}}]{\mathrm{2}\pi{x}}}{\mathrm{e}}\:=\frac{\mathrm{1}}{\mathrm{e}} \\ $$
Commented by greg_ed last updated on 31/May/21

$$\mathrm{ok}\:! \\ $$
