Question Number 69809 by RAKESH MANDA last updated on 28/Sep/19
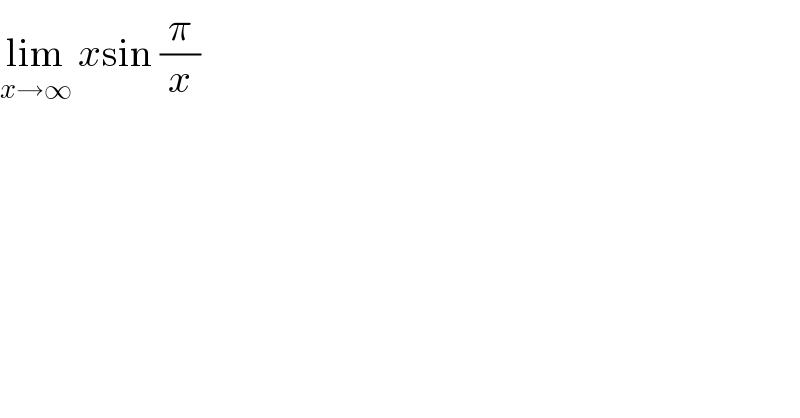
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{x}\mathrm{sin}\:\frac{\pi}{{x}} \\ $$
Commented by mr W last updated on 28/Sep/19
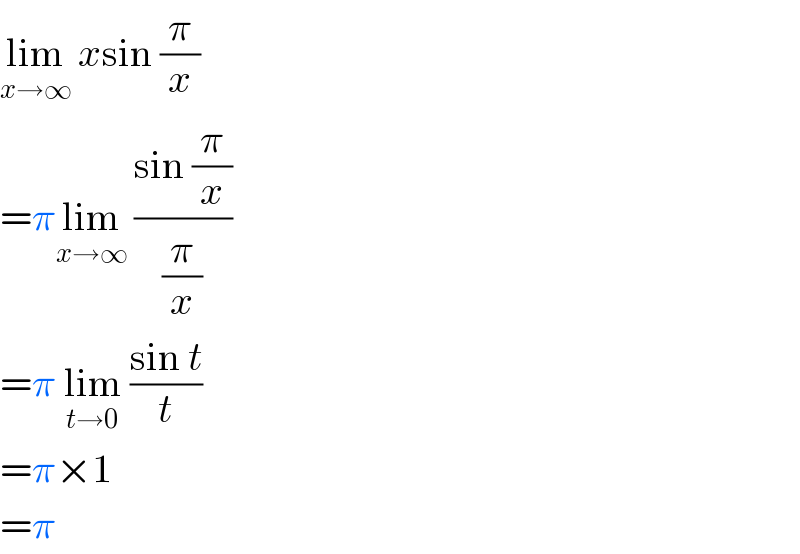
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{x}\mathrm{sin}\:\frac{\pi}{{x}} \\ $$$$=\pi\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\frac{\pi}{{x}}}{\frac{\pi}{{x}}} \\ $$$$=\pi\:\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:{t}}{{t}} \\ $$$$=\pi×\mathrm{1} \\ $$$$=\pi \\ $$
Commented by peter frank last updated on 28/Sep/19

$${thank}\:{you} \\ $$
Answered by $@ty@m123 last updated on 28/Sep/19
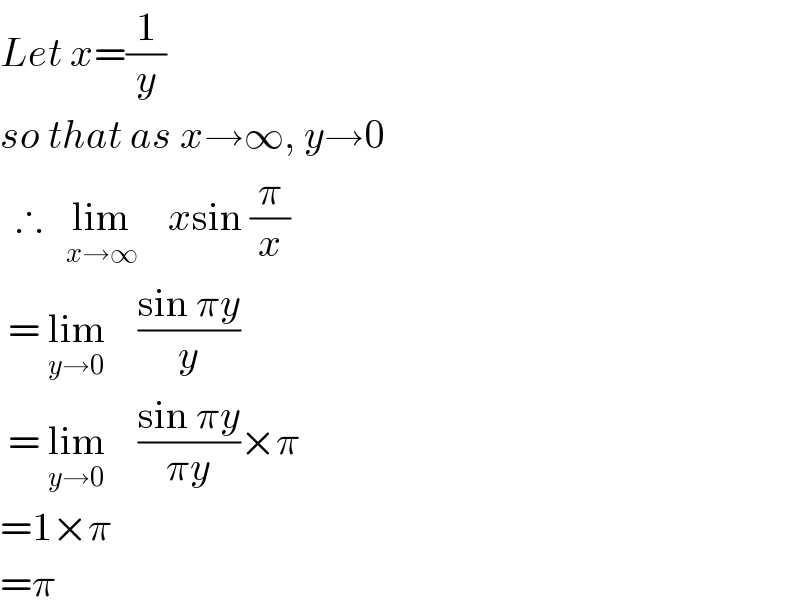
$${Let}\:{x}=\frac{\mathrm{1}}{{y}} \\ $$$${so}\:{that}\:{as}\:{x}\rightarrow\infty,\:{y}\rightarrow\mathrm{0} \\ $$$$\:\:\therefore\:\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\:\:\:{x}\mathrm{sin}\:\frac{\pi}{{x}} \\ $$$$\:=\:\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\:\:\frac{\mathrm{sin}\:\pi{y}}{{y}} \\ $$$$\:=\:\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\:\:\frac{\mathrm{sin}\:\pi{y}}{\pi{y}}×\pi \\ $$$$=\mathrm{1}×\pi \\ $$$$=\pi \\ $$
Answered by malwaan last updated on 28/Sep/19
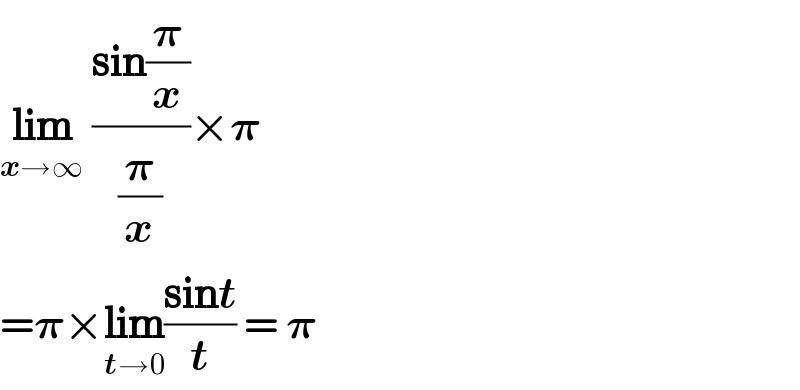
$$\underset{\boldsymbol{{x}}\rightarrow\infty} {\boldsymbol{\mathrm{lim}}}\:\frac{\boldsymbol{\mathrm{sin}}\frac{\boldsymbol{\pi}}{\boldsymbol{{x}}}}{\frac{\boldsymbol{\pi}}{\boldsymbol{{x}}}}×\boldsymbol{\pi} \\ $$$$=\boldsymbol{\pi}×\underset{\boldsymbol{{t}}\rightarrow\mathrm{0}} {\boldsymbol{\mathrm{lim}}}\frac{\boldsymbol{\mathrm{sin}{t}}}{\boldsymbol{{t}}}\:=\:\boldsymbol{\pi} \\ $$
Commented by malwaan last updated on 28/Sep/19
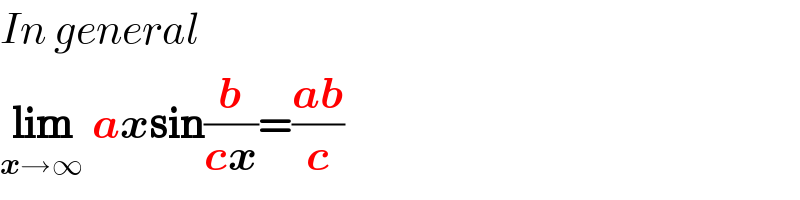
$${In}\:{general}\: \\ $$$$\underset{\boldsymbol{{x}}\rightarrow\infty} {\boldsymbol{\mathrm{lim}}}\:\boldsymbol{{ax}\mathrm{sin}}\frac{\boldsymbol{{b}}}{\boldsymbol{{cx}}}=\frac{\boldsymbol{{ab}}}{\boldsymbol{{c}}} \\ $$
