Question Number 68354 by TawaTawa last updated on 09/Sep/19
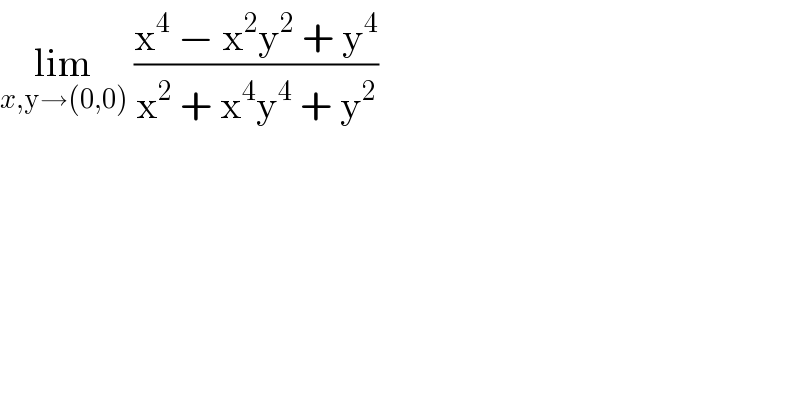
$$\underset{{x},\mathrm{y}\rightarrow\left(\mathrm{0},\mathrm{0}\right)} {\mathrm{lim}}\:\frac{\mathrm{x}^{\mathrm{4}} \:−\:\mathrm{x}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} \:+\:\mathrm{y}^{\mathrm{4}} }{\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{x}^{\mathrm{4}} \mathrm{y}^{\mathrm{4}} \:+\:\mathrm{y}^{\mathrm{2}} } \\ $$
Commented by kaivan.ahmadi last updated on 09/Sep/19
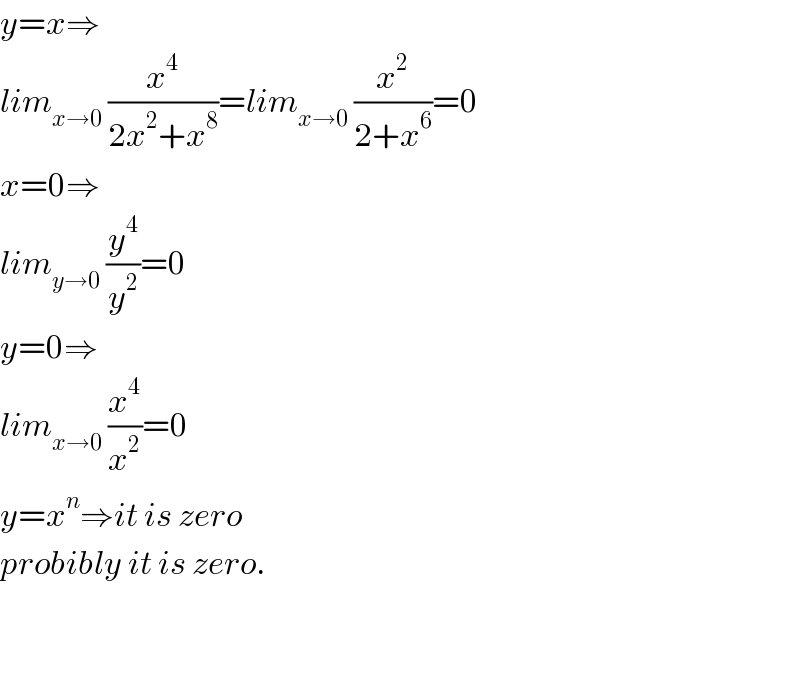
$${y}={x}\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \:\frac{{x}^{\mathrm{4}} }{\mathrm{2}{x}^{\mathrm{2}} +{x}^{\mathrm{8}} }={lim}_{{x}\rightarrow\mathrm{0}} \:\frac{{x}^{\mathrm{2}} }{\mathrm{2}+{x}^{\mathrm{6}} }=\mathrm{0} \\ $$$${x}=\mathrm{0}\Rightarrow \\ $$$${lim}_{{y}\rightarrow\mathrm{0}} \:\frac{{y}^{\mathrm{4}} }{{y}^{\mathrm{2}} }=\mathrm{0} \\ $$$${y}=\mathrm{0}\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \:\frac{{x}^{\mathrm{4}} }{{x}^{\mathrm{2}} }=\mathrm{0} \\ $$$${y}={x}^{{n}} \Rightarrow{it}\:{is}\:{zero} \\ $$$${probibly}\:{it}\:{is}\:{zero}. \\ $$$$ \\ $$$$ \\ $$
Commented by MJS last updated on 09/Sep/19
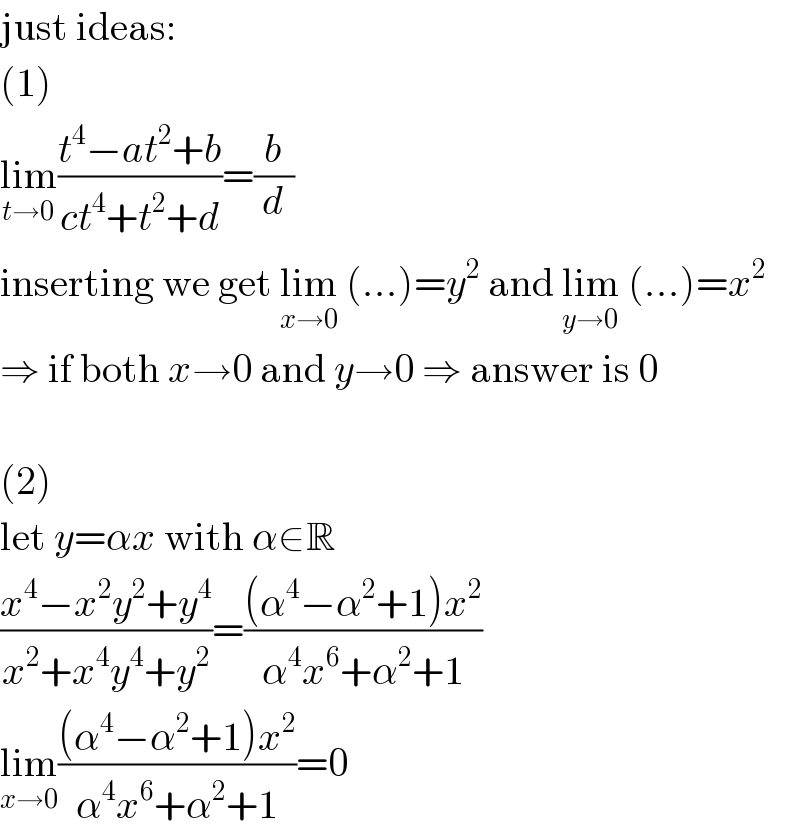
$$\mathrm{just}\:\mathrm{ideas}: \\ $$$$\left(\mathrm{1}\right) \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{t}^{\mathrm{4}} −{at}^{\mathrm{2}} +{b}}{{ct}^{\mathrm{4}} +{t}^{\mathrm{2}} +{d}}=\frac{{b}}{{d}} \\ $$$$\mathrm{inserting}\:\mathrm{we}\:\mathrm{get}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(…\right)={y}^{\mathrm{2}} \:\mathrm{and}\:\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(…\right)={x}^{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{if}\:\mathrm{both}\:{x}\rightarrow\mathrm{0}\:\mathrm{and}\:{y}\rightarrow\mathrm{0}\:\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\mathrm{0} \\ $$$$ \\ $$$$\left(\mathrm{2}\right) \\ $$$$\mathrm{let}\:{y}=\alpha{x}\:\mathrm{with}\:\alpha\in\mathbb{R} \\ $$$$\frac{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} {y}^{\mathrm{2}} +{y}^{\mathrm{4}} }{{x}^{\mathrm{2}} +{x}^{\mathrm{4}} {y}^{\mathrm{4}} +{y}^{\mathrm{2}} }=\frac{\left(\alpha^{\mathrm{4}} −\alpha^{\mathrm{2}} +\mathrm{1}\right){x}^{\mathrm{2}} }{\alpha^{\mathrm{4}} {x}^{\mathrm{6}} +\alpha^{\mathrm{2}} +\mathrm{1}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\alpha^{\mathrm{4}} −\alpha^{\mathrm{2}} +\mathrm{1}\right){x}^{\mathrm{2}} }{\alpha^{\mathrm{4}} {x}^{\mathrm{6}} +\alpha^{\mathrm{2}} +\mathrm{1}}=\mathrm{0} \\ $$
Commented by TawaTawa last updated on 09/Sep/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sirs} \\ $$
Commented by mind is power last updated on 09/Sep/19
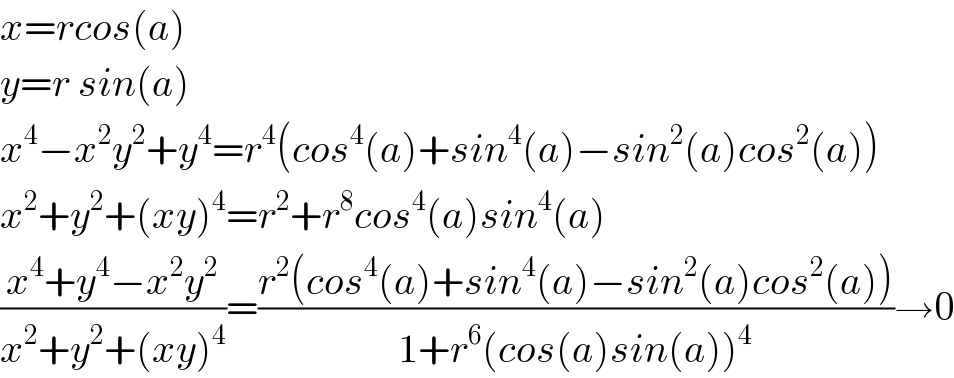
$${x}={rcos}\left({a}\right) \\ $$$${y}={r}\:{sin}\left({a}\right) \\ $$$${x}^{\mathrm{4}} −{x}^{\mathrm{2}} {y}^{\mathrm{2}} +{y}^{\mathrm{4}} ={r}^{\mathrm{4}} \left({cos}^{\mathrm{4}} \left({a}\right)+{sin}^{\mathrm{4}} \left({a}\right)−{sin}^{\mathrm{2}} \left({a}\right){cos}^{\mathrm{2}} \left({a}\right)\right) \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\left({xy}\right)^{\mathrm{4}} ={r}^{\mathrm{2}} +{r}^{\mathrm{8}} {cos}^{\mathrm{4}} \left({a}\right){sin}^{\mathrm{4}} \left({a}\right) \\ $$$$\frac{{x}^{\mathrm{4}} +{y}^{\mathrm{4}} −{x}^{\mathrm{2}} {y}^{\mathrm{2}} }{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\left({xy}\right)^{\mathrm{4}} }=\frac{{r}^{\mathrm{2}} \left({cos}^{\mathrm{4}} \left({a}\right)+{sin}^{\mathrm{4}} \left({a}\right)−{sin}^{\mathrm{2}} \left({a}\right){cos}^{\mathrm{2}} \left({a}\right)\right)}{\mathrm{1}+{r}^{\mathrm{6}} \left({cos}\left({a}\right){sin}\left({a}\right)\right)^{\mathrm{4}} }\rightarrow\mathrm{0} \\ $$
Commented by TawaTawa last updated on 10/Sep/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by mind is power last updated on 10/Sep/19

$${y},{re}\:{welcom} \\ $$
