Question Number 2888 by prakash jain last updated on 29/Nov/15
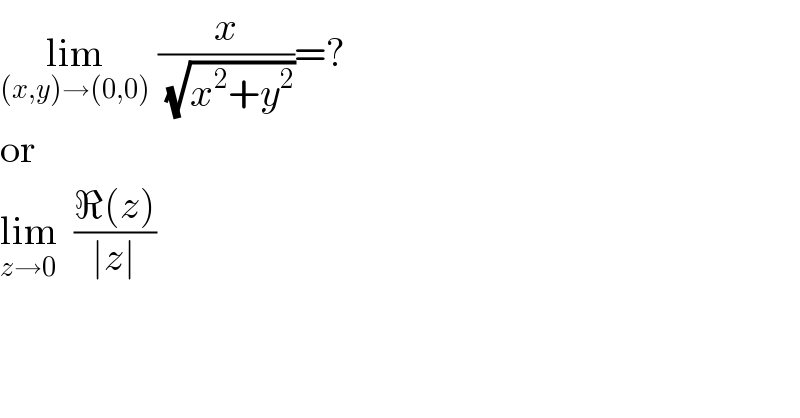
$$\underset{\left({x},{y}\right)\rightarrow\left(\mathrm{0},\mathrm{0}\right)} {\mathrm{lim}}\:\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }}=? \\ $$$$\mathrm{or} \\ $$$$\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{\Re\left({z}\right)}{\mid{z}\mid} \\ $$
Answered by prakash jain last updated on 29/Nov/15
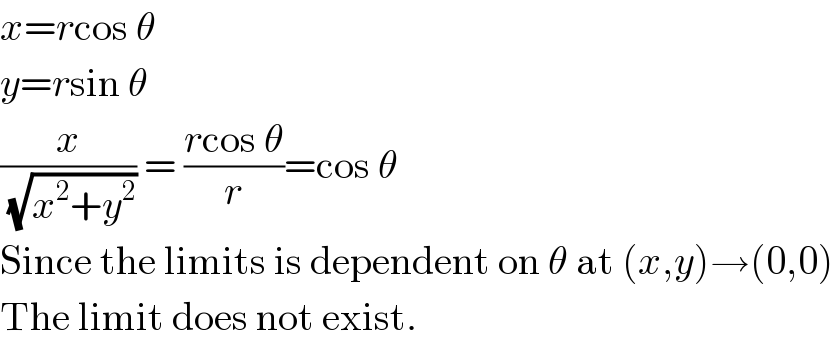
$${x}={r}\mathrm{cos}\:\theta \\ $$$${y}={r}\mathrm{sin}\:\theta \\ $$$$\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }}\:=\:\frac{{r}\mathrm{cos}\:\theta}{{r}}=\mathrm{cos}\:\theta \\ $$$$\mathrm{Since}\:\mathrm{the}\:\mathrm{limits}\:\mathrm{is}\:\mathrm{dependent}\:\mathrm{on}\:\theta\:\mathrm{at}\:\left({x},{y}\right)\rightarrow\left(\mathrm{0},\mathrm{0}\right) \\ $$$$\mathrm{The}\:\mathrm{limit}\:\mathrm{does}\:\mathrm{not}\:\mathrm{exist}. \\ $$
