Question Number 12062 by tawa last updated on 10/Apr/17
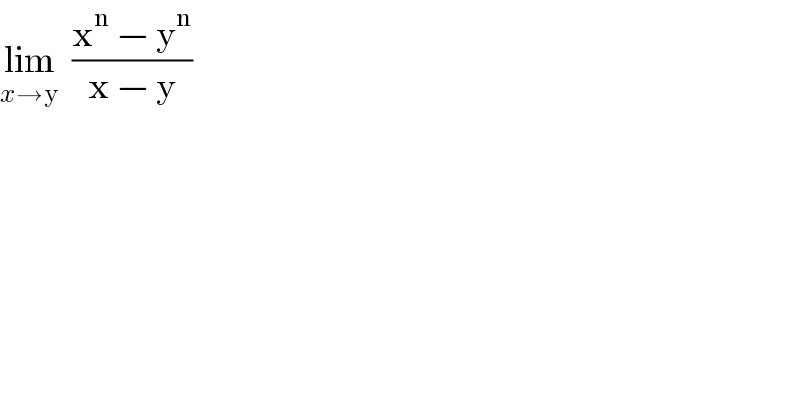
$$\underset{{x}\rightarrow\mathrm{y}} {\mathrm{lim}}\:\:\frac{\mathrm{x}^{\mathrm{n}} \:−\:\mathrm{y}^{\mathrm{n}} }{\mathrm{x}\:−\:\mathrm{y}} \\ $$
Answered by ajfour last updated on 11/Apr/17
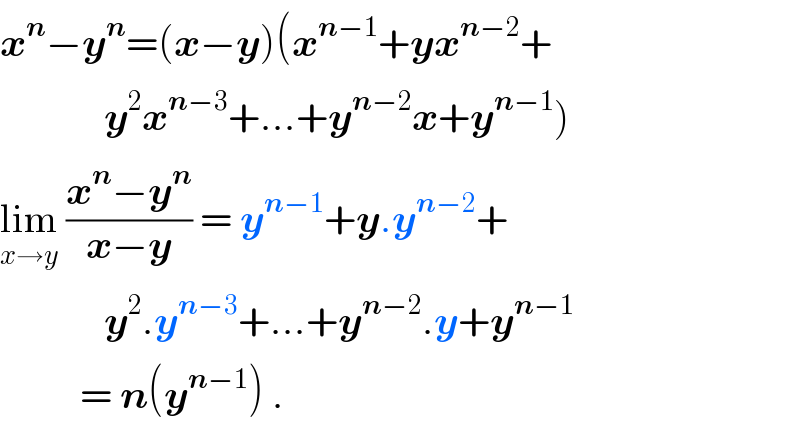
$$\boldsymbol{{x}}^{\boldsymbol{{n}}} −\boldsymbol{{y}}^{\boldsymbol{{n}}} =\left(\boldsymbol{{x}}−\boldsymbol{{y}}\right)\left(\boldsymbol{{x}}^{\boldsymbol{{n}}−\mathrm{1}} +\boldsymbol{{yx}}^{\boldsymbol{{n}}−\mathrm{2}} +\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{y}}^{\mathrm{2}} \boldsymbol{{x}}^{\boldsymbol{{n}}−\mathrm{3}} +…+\boldsymbol{{y}}^{\boldsymbol{{n}}−\mathrm{2}} \boldsymbol{{x}}+\boldsymbol{{y}}^{\boldsymbol{{n}}−\mathrm{1}} \right) \\ $$$$\underset{{x}\rightarrow{y}} {\mathrm{lim}}\:\frac{\boldsymbol{{x}}^{\boldsymbol{{n}}} −\boldsymbol{{y}}^{\boldsymbol{{n}}} }{\boldsymbol{{x}}−\boldsymbol{{y}}}\:=\:\boldsymbol{{y}}^{\boldsymbol{{n}}−\mathrm{1}} +\boldsymbol{{y}}.\boldsymbol{{y}}^{\boldsymbol{{n}}−\mathrm{2}} + \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{y}}^{\mathrm{2}} .\boldsymbol{{y}}^{\boldsymbol{{n}}−\mathrm{3}} +…+\boldsymbol{{y}}^{\boldsymbol{{n}}−\mathrm{2}} .\boldsymbol{{y}}+\boldsymbol{{y}}^{\boldsymbol{{n}}−\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:\boldsymbol{{n}}\left(\boldsymbol{{y}}^{\boldsymbol{{n}}−\mathrm{1}} \right)\:. \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 11/Apr/17
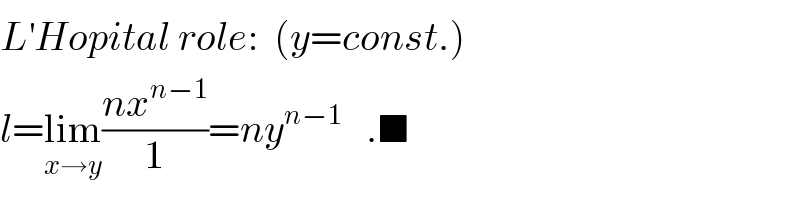
$${L}^{'} {Hopital}\:{role}:\:\:\left({y}={const}.\right) \\ $$$${l}=\underset{{x}\rightarrow{y}} {\mathrm{lim}}\frac{{nx}^{{n}−\mathrm{1}} }{\mathrm{1}}={ny}^{{n}−\mathrm{1}} \:\:\:.\blacksquare \\ $$
