Question Number 5637 by sanusihammed last updated on 23/May/16
![Limit [((3^(n+1) − 5^(n+1) )/(3^n − 5^n ))] x→∞ Please help. Thanks](https://www.tinkutara.com/question/Q5637.png)
$${Limit}\:\:\:\left[\frac{\mathrm{3}^{{n}+\mathrm{1}} \:−\:\mathrm{5}^{{n}+\mathrm{1}} }{\mathrm{3}^{{n}} \:−\:\mathrm{5}^{{n}} }\right] \\ $$$${x}\rightarrow\infty \\ $$$$ \\ $$$$ \\ $$$${Please}\:{help}.\:{Thanks} \\ $$
Answered by Yozzii last updated on 23/May/16
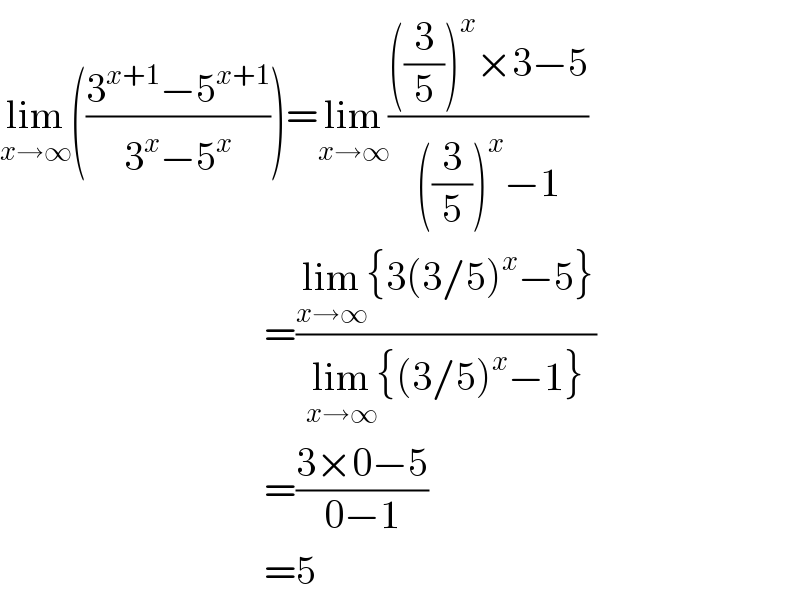
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{3}^{{x}+\mathrm{1}} −\mathrm{5}^{{x}+\mathrm{1}} }{\mathrm{3}^{{x}} −\mathrm{5}^{{x}} }\right)=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\left(\frac{\mathrm{3}}{\mathrm{5}}\right)^{{x}} ×\mathrm{3}−\mathrm{5}}{\left(\frac{\mathrm{3}}{\mathrm{5}}\right)^{{x}} −\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left\{\mathrm{3}\left(\mathrm{3}/\mathrm{5}\right)^{{x}} −\mathrm{5}\right\}}{\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left\{\left(\mathrm{3}/\mathrm{5}\right)^{{x}} −\mathrm{1}\right\}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{3}×\mathrm{0}−\mathrm{5}}{\mathrm{0}−\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{5} \\ $$
Commented by Rasheed Soomro last updated on 23/May/16

$$\mathcal{N}{i}\mathcal{CE}! \\ $$
Commented by sanusihammed last updated on 23/May/16
$${Thanks}\:{so}\:{much}\:{for}\:{your}\:{time} \\ $$
