Question Number 135223 by benjo_mathlover last updated on 11/Mar/21
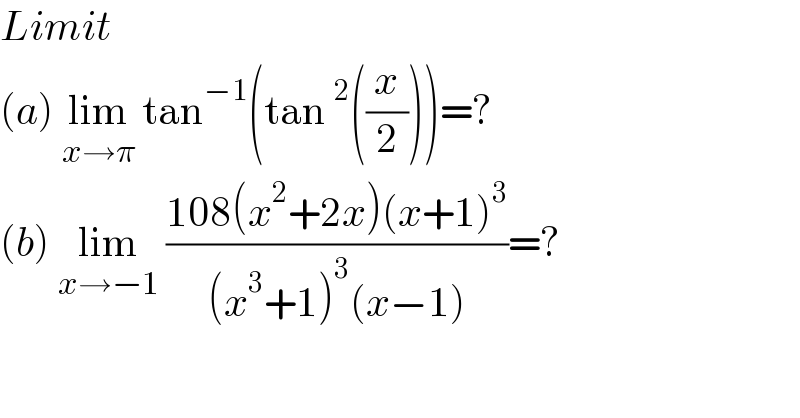
$${Limit}\: \\ $$$$\left({a}\right)\:\underset{{x}\rightarrow\pi} {\mathrm{lim}}\:\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{tan}\:^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\right)=? \\ $$$$\left({b}\right)\:\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{108}\left({x}^{\mathrm{2}} +\mathrm{2}{x}\right)\left({x}+\mathrm{1}\right)^{\mathrm{3}} }{\left({x}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{3}} \left({x}−\mathrm{1}\right)}=? \\ $$
Answered by EDWIN88 last updated on 11/Mar/21
![(b) lim_(x→−1) ((108(x^2 +2x))/(x−1)) × [ lim_(x→−1) ((x+1)/(x^3 +1)) ]^3 = ((108(−1))/(−2)) × [lim_(x→−1) ((x+1)/((x+1)(x^2 −x+1))) ]^3 = 54× [ lim_(x→−1) (1/(x^2 −x+1)) ]^3 = 54×(1/(27))=2](https://www.tinkutara.com/question/Q135224.png)
$$\left(\mathrm{b}\right)\:\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{108}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2x}\right)}{\mathrm{x}−\mathrm{1}}\:×\:\left[\:\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}^{\mathrm{3}} +\mathrm{1}}\:\right]^{\mathrm{3}} = \\ $$$$\frac{\mathrm{108}\left(−\mathrm{1}\right)}{−\mathrm{2}}\:×\:\left[\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{x}+\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)}\:\right]^{\mathrm{3}} = \\ $$$$\mathrm{54}×\:\left[\:\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}\:\right]^{\mathrm{3}} =\:\mathrm{54}×\frac{\mathrm{1}}{\mathrm{27}}=\mathrm{2} \\ $$
Answered by liberty last updated on 12/Mar/21
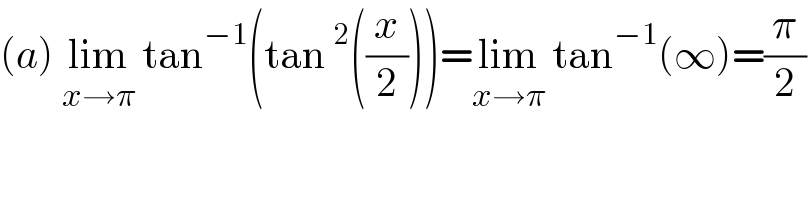
$$\left({a}\right)\:\underset{{x}\rightarrow\pi} {\mathrm{lim}}\:\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{tan}\:^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\right)=\underset{{x}\rightarrow\pi} {\mathrm{lim}}\:\mathrm{tan}^{−\mathrm{1}} \left(\infty\right)=\frac{\pi}{\mathrm{2}} \\ $$
