Question Number 137203 by mathocean1 last updated on 31/Mar/21
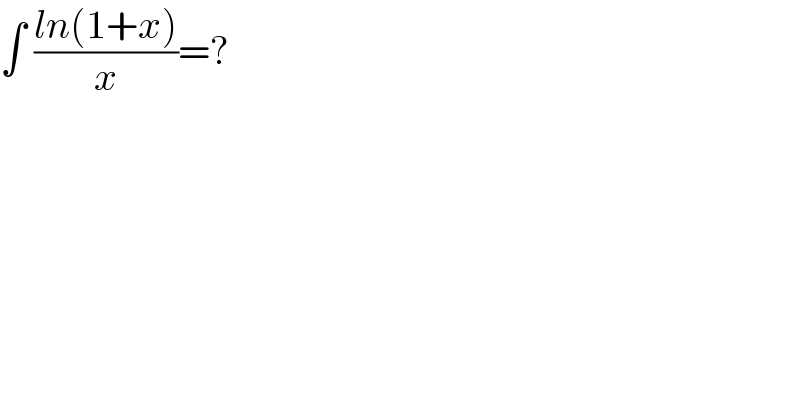
$$\int\:\frac{{ln}\left(\mathrm{1}+{x}\right)}{{x}}=? \\ $$
Answered by Dwaipayan Shikari last updated on 31/Mar/21
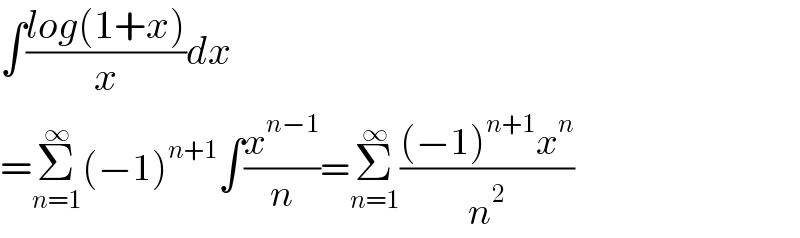
$$\int\frac{{log}\left(\mathrm{1}+{x}\right)}{{x}}{dx} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \int\frac{{x}^{{n}−\mathrm{1}} }{{n}}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {x}^{{n}} }{{n}^{\mathrm{2}} } \\ $$
Answered by Ar Brandon last updated on 31/Mar/21
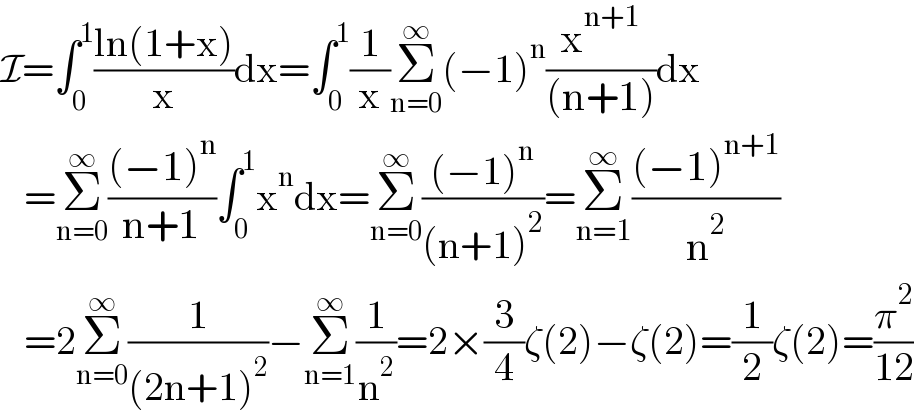
$$\mathcal{I}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{x}}\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{n}} \frac{\mathrm{x}^{\mathrm{n}+\mathrm{1}} }{\left(\mathrm{n}+\mathrm{1}\right)}\mathrm{dx} \\ $$$$\:\:\:=\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}+\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}^{\mathrm{n}} \mathrm{dx}=\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }=\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}^{\mathrm{2}} } \\ $$$$\:\:\:=\mathrm{2}\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} }−\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }=\mathrm{2}×\frac{\mathrm{3}}{\mathrm{4}}\zeta\left(\mathrm{2}\right)−\zeta\left(\mathrm{2}\right)=\frac{\mathrm{1}}{\mathrm{2}}\zeta\left(\mathrm{2}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$
