Question Number 74542 by Cmr 237 last updated on 25/Nov/19
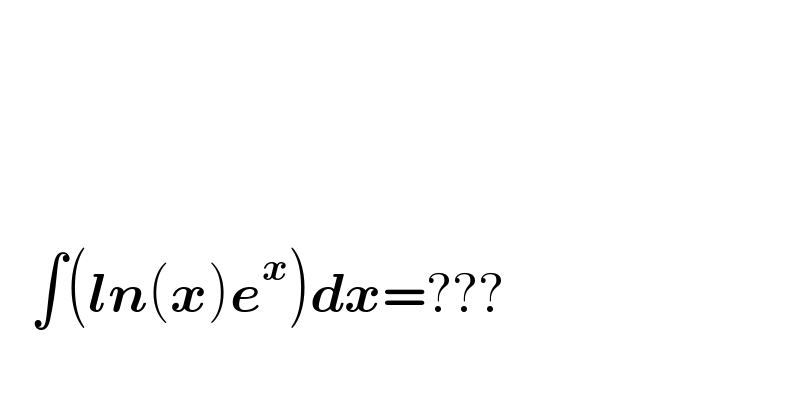
$$ \\ $$$$ \\ $$$$ \\ $$$$\:\:\:\int\left(\boldsymbol{{ln}}\left(\boldsymbol{{x}}\right)\boldsymbol{{e}}^{\boldsymbol{{x}}} \right)\boldsymbol{{dx}}=??? \\ $$
Answered by MJS last updated on 25/Nov/19

$$\mathrm{by}\:\mathrm{parts} \\ $$$${u}=\mathrm{ln}\:{x}\:\Rightarrow\:{u}'=\frac{\mathrm{1}}{{x}} \\ $$$${v}'={v}=\mathrm{e}^{{x}} \\ $$$$\int\mathrm{e}^{{x}} \mathrm{ln}\:{x}\:{dx}=\mathrm{e}^{{x}} \mathrm{ln}\:{x}\:−\int\frac{\mathrm{e}^{{x}} }{{x}}{dx}= \\ $$$$=\mathrm{e}^{{x}} \mathrm{ln}\:{x}\:−\mathrm{Ei}\:{x}\:+{C} \\ $$$$\mathrm{Ei}\:\left({x}\right)\:\mathrm{is}\:\mathrm{the}\:\mathrm{Integral}−\mathrm{Exponential}\:\mathrm{Function} \\ $$$$\mathrm{please}\:\mathrm{search}\:\mathrm{the}\:\mathrm{web}\:\mathrm{for}\:\mathrm{details} \\ $$
