Question Number 71850 by SmNayon11 last updated on 21/Oct/19
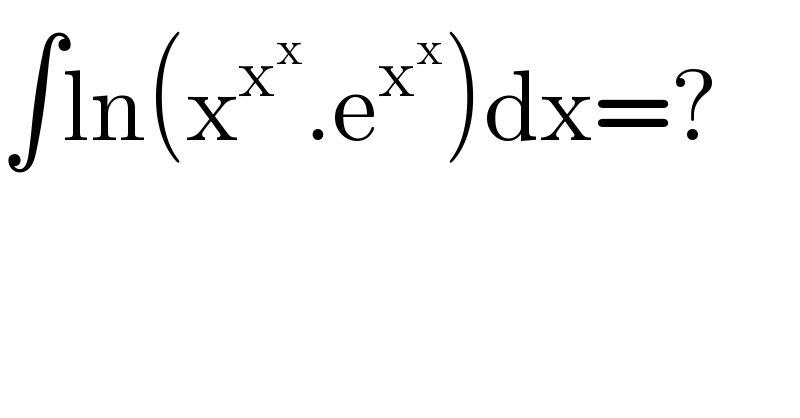
$$\int\mathrm{ln}\left(\mathrm{x}^{\mathrm{x}^{\mathrm{x}} } .\mathrm{e}^{\mathrm{x}^{\mathrm{x}} } \right)\mathrm{dx}=? \\ $$
Answered by MJS last updated on 21/Oct/19
![∫ln (x^x^x e^x^x )dx=∫x^x (1+ln x)dx= [t=x^x → dx=(dt/(x^x (1+ln x)))] =∫dt=t=x^x +C](https://www.tinkutara.com/question/Q71861.png)
$$\int\mathrm{ln}\:\left({x}^{{x}^{{x}} } \mathrm{e}^{{x}^{{x}} } \right){dx}=\int{x}^{{x}} \left(\mathrm{1}+\mathrm{ln}\:{x}\right){dx}= \\ $$$$\:\:\:\:\:\left[{t}={x}^{{x}} \:\rightarrow\:{dx}=\frac{{dt}}{{x}^{{x}} \left(\mathrm{1}+\mathrm{ln}\:{x}\right)}\right] \\ $$$$=\int{dt}={t}={x}^{{x}} +{C} \\ $$
Answered by mind is power last updated on 21/Oct/19
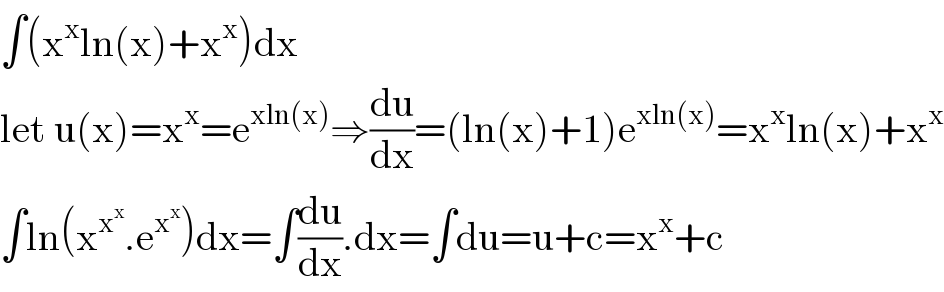
$$\int\left(\mathrm{x}^{\mathrm{x}} \mathrm{ln}\left(\mathrm{x}\right)+\mathrm{x}^{\mathrm{x}} \right)\mathrm{dx} \\ $$$$\mathrm{let}\:\mathrm{u}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{x}} =\mathrm{e}^{\mathrm{xln}\left(\mathrm{x}\right)} \Rightarrow\frac{\mathrm{du}}{\mathrm{dx}}=\left(\mathrm{ln}\left(\mathrm{x}\right)+\mathrm{1}\right)\mathrm{e}^{\mathrm{xln}\left(\mathrm{x}\right)} =\mathrm{x}^{\mathrm{x}} \mathrm{ln}\left(\mathrm{x}\right)+\mathrm{x}^{\mathrm{x}} \\ $$$$\int\mathrm{ln}\left(\mathrm{x}^{\mathrm{x}^{\mathrm{x}} } .\mathrm{e}^{\mathrm{x}^{\mathrm{x}} } \right)\mathrm{dx}=\int\frac{\mathrm{du}}{\mathrm{dx}}.\mathrm{dx}=\int\mathrm{du}=\mathrm{u}+\mathrm{c}=\mathrm{x}^{\mathrm{x}} +\mathrm{c} \\ $$
