Question Number 70483 by Mikaell last updated on 04/Oct/19
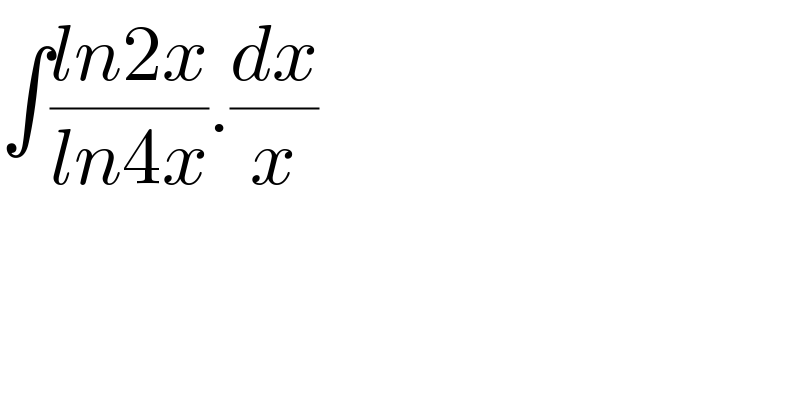
$$\int\frac{{ln}\mathrm{2}{x}}{{ln}\mathrm{4}{x}}.\frac{{dx}}{{x}} \\ $$
Commented by peter frank last updated on 04/Oct/19

$${thankx} \\ $$
Commented by kaivan.ahmadi last updated on 04/Oct/19
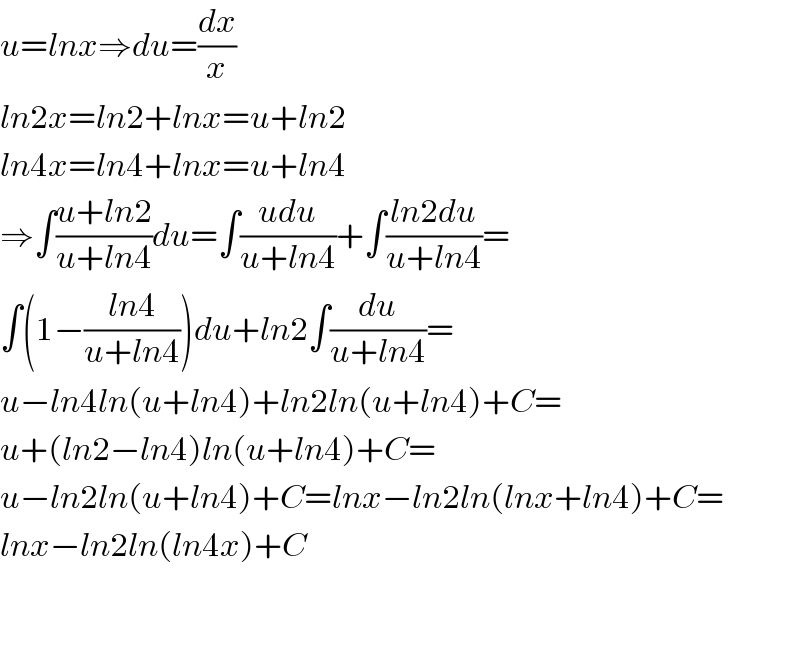
$${u}={lnx}\Rightarrow{du}=\frac{{dx}}{{x}} \\ $$$${ln}\mathrm{2}{x}={ln}\mathrm{2}+{lnx}={u}+{ln}\mathrm{2} \\ $$$${ln}\mathrm{4}{x}={ln}\mathrm{4}+{lnx}={u}+{ln}\mathrm{4} \\ $$$$\Rightarrow\int\frac{{u}+{ln}\mathrm{2}}{{u}+{ln}\mathrm{4}}{du}=\int\frac{{udu}}{{u}+{ln}\mathrm{4}}+\int\frac{{ln}\mathrm{2}{du}}{{u}+{ln}\mathrm{4}}= \\ $$$$\int\left(\mathrm{1}−\frac{{ln}\mathrm{4}}{{u}+{ln}\mathrm{4}}\right){du}+{ln}\mathrm{2}\int\frac{{du}}{{u}+{ln}\mathrm{4}}= \\ $$$${u}−{ln}\mathrm{4}{ln}\left({u}+{ln}\mathrm{4}\right)+{ln}\mathrm{2}{ln}\left({u}+{ln}\mathrm{4}\right)+{C}= \\ $$$${u}+\left({ln}\mathrm{2}−{ln}\mathrm{4}\right){ln}\left({u}+{ln}\mathrm{4}\right)+{C}= \\ $$$${u}−{ln}\mathrm{2}{ln}\left({u}+{ln}\mathrm{4}\right)+{C}={lnx}−{ln}\mathrm{2}{ln}\left({lnx}+{ln}\mathrm{4}\right)+{C}= \\ $$$${lnx}−{ln}\mathrm{2}{ln}\left({ln}\mathrm{4}{x}\right)+{C} \\ $$$$ \\ $$$$ \\ $$
Commented by Mikaell last updated on 04/Oct/19
$${thank}\:{you}\:{Sir} \\ $$
Answered by Tanmay chaudhury last updated on 04/Oct/19
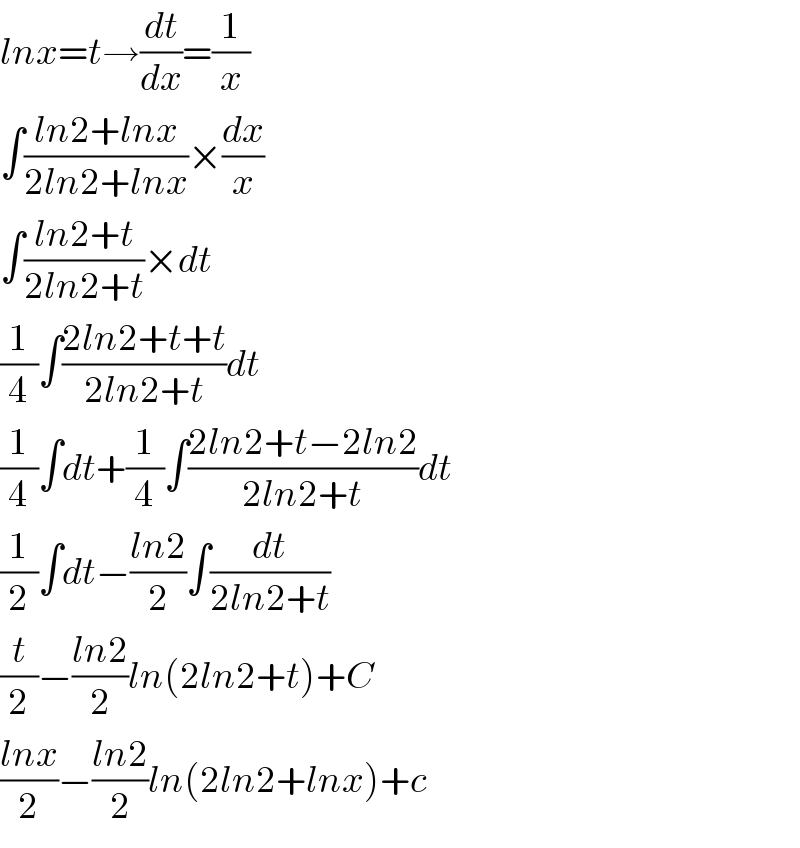
$${lnx}={t}\rightarrow\frac{{dt}}{{dx}}=\frac{\mathrm{1}}{{x}} \\ $$$$\int\frac{{ln}\mathrm{2}+{lnx}}{\mathrm{2}{ln}\mathrm{2}+{lnx}}×\frac{{dx}}{{x}} \\ $$$$\int\frac{{ln}\mathrm{2}+{t}}{\mathrm{2}{ln}\mathrm{2}+{t}}×{dt} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{2}{ln}\mathrm{2}+{t}+{t}}{\mathrm{2}{ln}\mathrm{2}+{t}}{dt} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\int{dt}+\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{2}{ln}\mathrm{2}+{t}−\mathrm{2}{ln}\mathrm{2}}{\mathrm{2}{ln}\mathrm{2}+{t}}{dt} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int{dt}−\frac{{ln}\mathrm{2}}{\mathrm{2}}\int\frac{{dt}}{\mathrm{2}{ln}\mathrm{2}+{t}} \\ $$$$\frac{{t}}{\mathrm{2}}−\frac{{ln}\mathrm{2}}{\mathrm{2}}{ln}\left(\mathrm{2}{ln}\mathrm{2}+{t}\right)+{C} \\ $$$$\frac{{lnx}}{\mathrm{2}}−\frac{{ln}\mathrm{2}}{\mathrm{2}}{ln}\left(\mathrm{2}{ln}\mathrm{2}+{lnx}\right)+{c} \\ $$
Commented by peter frank last updated on 04/Oct/19

$${thanx} \\ $$
Commented by Mikaell last updated on 04/Oct/19

$${thank}\:{you}\:{Sir} \\ $$
