Question Number 4458 by love math last updated on 29/Jan/16
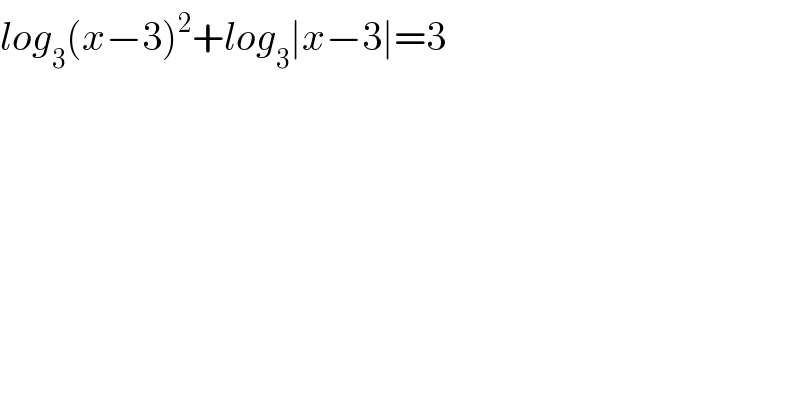
$${log}_{\mathrm{3}} \left({x}−\mathrm{3}\right)^{\mathrm{2}} +{log}_{\mathrm{3}} \mid{x}−\mathrm{3}\mid=\mathrm{3} \\ $$
Answered by Yozzii last updated on 29/Jan/16
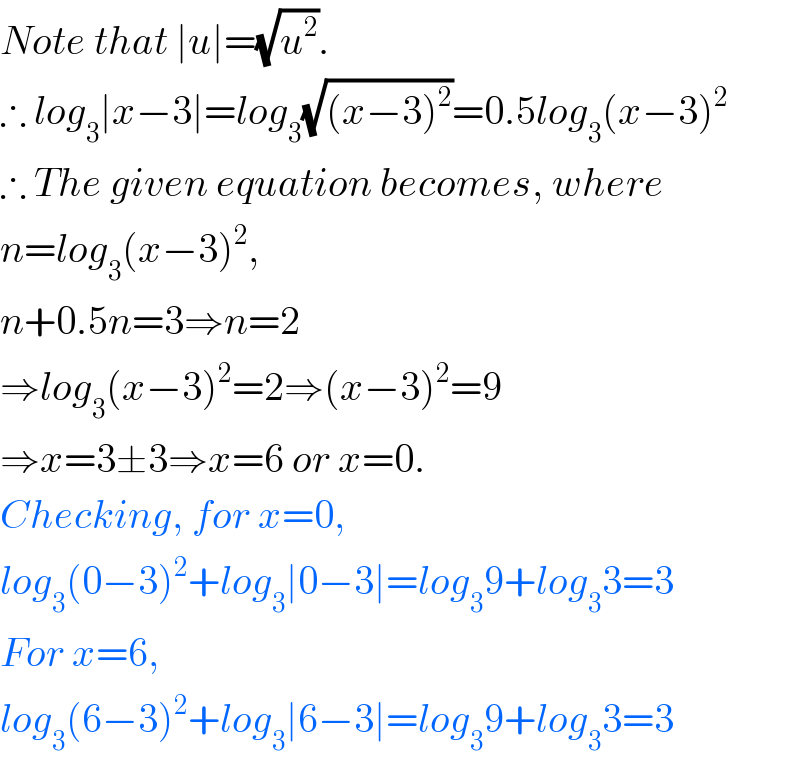
$${Note}\:{that}\:\mid{u}\mid=\sqrt{{u}^{\mathrm{2}} }. \\ $$$$\therefore\:{log}_{\mathrm{3}} \mid{x}−\mathrm{3}\mid={log}_{\mathrm{3}} \sqrt{\left({x}−\mathrm{3}\right)^{\mathrm{2}} }=\mathrm{0}.\mathrm{5}{log}_{\mathrm{3}} \left({x}−\mathrm{3}\right)^{\mathrm{2}} \\ $$$$\therefore\:{The}\:{given}\:{equation}\:{becomes},\:{where} \\ $$$${n}={log}_{\mathrm{3}} \left({x}−\mathrm{3}\right)^{\mathrm{2}} , \\ $$$${n}+\mathrm{0}.\mathrm{5}{n}=\mathrm{3}\Rightarrow{n}=\mathrm{2} \\ $$$$\Rightarrow{log}_{\mathrm{3}} \left({x}−\mathrm{3}\right)^{\mathrm{2}} =\mathrm{2}\Rightarrow\left({x}−\mathrm{3}\right)^{\mathrm{2}} =\mathrm{9} \\ $$$$\Rightarrow{x}=\mathrm{3}\pm\mathrm{3}\Rightarrow{x}=\mathrm{6}\:{or}\:{x}=\mathrm{0}.\: \\ $$$${Checking},\:{for}\:{x}=\mathrm{0}, \\ $$$${log}_{\mathrm{3}} \left(\mathrm{0}−\mathrm{3}\right)^{\mathrm{2}} +{log}_{\mathrm{3}} \mid\mathrm{0}−\mathrm{3}\mid={log}_{\mathrm{3}} \mathrm{9}+{log}_{\mathrm{3}} \mathrm{3}=\mathrm{3} \\ $$$${For}\:{x}=\mathrm{6},\: \\ $$$${log}_{\mathrm{3}} \left(\mathrm{6}−\mathrm{3}\right)^{\mathrm{2}} +{log}_{\mathrm{3}} \mid\mathrm{6}−\mathrm{3}\mid={log}_{\mathrm{3}} \mathrm{9}+{log}_{\mathrm{3}} \mathrm{3}=\mathrm{3} \\ $$
Commented by Yozzii last updated on 29/Jan/16
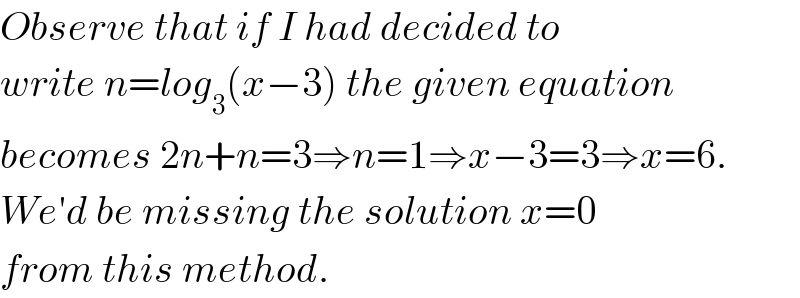
$${Observe}\:{that}\:{if}\:{I}\:{had}\:{decided}\:{to}\: \\ $$$${write}\:{n}={log}_{\mathrm{3}} \left({x}−\mathrm{3}\right)\:{the}\:{given}\:{equation} \\ $$$${becomes}\:\mathrm{2}{n}+{n}=\mathrm{3}\Rightarrow{n}=\mathrm{1}\Rightarrow{x}−\mathrm{3}=\mathrm{3}\Rightarrow{x}=\mathrm{6}. \\ $$$${We}'{d}\:{be}\:{missing}\:{the}\:{solution}\:{x}=\mathrm{0} \\ $$$${from}\:{this}\:{method}. \\ $$
Commented by Rasheed Soomro last updated on 31/Jan/16

$$\mathcal{N}^{\:} {ic}\mathcal{E}! \\ $$
