Menu Close

log-x-8-x-2-3x-4-lt-2-log-4-x-2-x-4-

Tinku Tara 0 Comments
Pin




Question Number 133936 by liberty last updated on 25/Feb/21
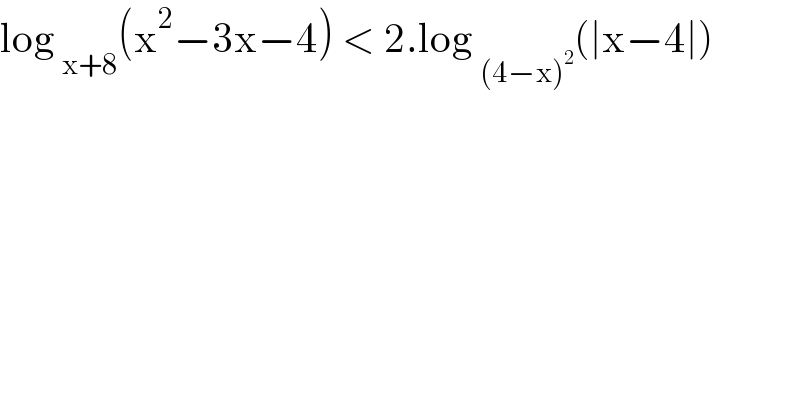
log _(x+8) (x^2 −3x−4) < 2.log _((4−x)^2 ) (∣x−4∣)
$$\mathrm{log}\:_{\mathrm{x}+\mathrm{8}} \left(\mathrm{x}^{\mathrm{2}} −\mathrm{3x}−\mathrm{4}\right)\:<\:\mathrm{2}.\mathrm{log}\:_{\left(\mathrm{4}−\mathrm{x}\right)^{\mathrm{2}} } \left(\mid\mathrm{x}−\mathrm{4}\mid\right)\: \\ $$
Answered by EDWIN88 last updated on 25/Feb/21
log _(x+8) (x^2 −3x−4)<2.log _((4−x)^2 ) (∣x−4∣) { ((x^2 −3x−4>0)),((x+8>0 ; x+8≠1 )),(((4−x)^2 ≠1 , x≠4 )) :} { ((x<−1 ; x>4)),((x>−8)),((x≠4; x≠3; x≠5)) :} ⇔ log _(x+8) (x^2 −3x−4)<2.log _((x−4)^2 ) ∣x−4∣ ⇔log _(x+8) (x^2 −3x−4)<2.(1/2)log _(∣x−4∣) ∣x−4∣ ⇔ log _(x+8) (x^2 −3x−4)<1 ; ((ln (x^2 −3x−4))/(ln (x+8))) <1 ((ln (x^2 −3x−4)−ln (x+8))/(ln (x+8))) <0 numerator :ln (x^2 −3x−4) = ln (x+8) ; x^2 −4x−12=0 x_1 =6 ; x_2 =−2 denumerator : ln (x+8)=0 ; x=−7 solution set is (−8;−7)∪(−2;−1)∪(4;5)∪(5;6)
$$\:\mathrm{log}\:_{\mathrm{x}+\mathrm{8}} \left(\mathrm{x}^{\mathrm{2}} −\mathrm{3x}−\mathrm{4}\right)<\mathrm{2}.\mathrm{log}\:_{\left(\mathrm{4}−\mathrm{x}\right)^{\mathrm{2}} } \left(\mid\mathrm{x}−\mathrm{4}\mid\right) \\ $$$$\begin{cases}{\mathrm{x}^{\mathrm{2}} −\mathrm{3x}−\mathrm{4}>\mathrm{0}}\\{\mathrm{x}+\mathrm{8}>\mathrm{0}\:;\:\mathrm{x}+\mathrm{8}\neq\mathrm{1}\:}\\{\left(\mathrm{4}−\mathrm{x}\right)^{\mathrm{2}} \neq\mathrm{1}\:,\:\mathrm{x}\neq\mathrm{4}\:}\end{cases}\:\begin{cases}{\mathrm{x}<−\mathrm{1}\:;\:\mathrm{x}>\mathrm{4}}\\{\mathrm{x}>−\mathrm{8}}\\{\mathrm{x}\neq\mathrm{4};\:\mathrm{x}\neq\mathrm{3};\:\mathrm{x}\neq\mathrm{5}}\end{cases} \\ $$$$\Leftrightarrow\:\mathrm{log}\:_{\mathrm{x}+\mathrm{8}} \left(\mathrm{x}^{\mathrm{2}} −\mathrm{3x}−\mathrm{4}\right)<\mathrm{2}.\mathrm{log}\:_{\left(\mathrm{x}−\mathrm{4}\right)^{\mathrm{2}} } \mid\mathrm{x}−\mathrm{4}\mid \\ $$$$\Leftrightarrow\mathrm{log}\:_{\mathrm{x}+\mathrm{8}} \left(\mathrm{x}^{\mathrm{2}} −\mathrm{3x}−\mathrm{4}\right)<\mathrm{2}.\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\:_{\mid\mathrm{x}−\mathrm{4}\mid} \:\mid\mathrm{x}−\mathrm{4}\mid \\ $$$$\Leftrightarrow\:\mathrm{log}\underset{\mathrm{x}+\mathrm{8}} {\:}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{3x}−\mathrm{4}\right)<\mathrm{1}\:;\:\frac{\mathrm{ln}\:\left(\mathrm{x}^{\mathrm{2}} −\mathrm{3x}−\mathrm{4}\right)}{\mathrm{ln}\:\left(\mathrm{x}+\mathrm{8}\right)}\:<\mathrm{1} \\ $$$$\:\frac{\mathrm{ln}\:\left(\mathrm{x}^{\mathrm{2}} −\mathrm{3x}−\mathrm{4}\right)−\mathrm{ln}\:\left(\mathrm{x}+\mathrm{8}\right)}{\mathrm{ln}\:\left(\mathrm{x}+\mathrm{8}\right)}\:<\mathrm{0} \\ $$$$\mathrm{numerator}\::\mathrm{ln}\:\left(\mathrm{x}^{\mathrm{2}} −\mathrm{3x}−\mathrm{4}\right)\:=\:\mathrm{ln}\:\left(\mathrm{x}+\mathrm{8}\right)\:;\:\mathrm{x}^{\mathrm{2}} −\mathrm{4x}−\mathrm{12}=\mathrm{0} \\ $$$$\mathrm{x}_{\mathrm{1}} =\mathrm{6}\:;\:\mathrm{x}_{\mathrm{2}} =−\mathrm{2} \\ $$$$\mathrm{denumerator}\::\:\mathrm{ln}\:\left(\mathrm{x}+\mathrm{8}\right)=\mathrm{0}\:;\:\mathrm{x}=−\mathrm{7} \\ $$$$\mathrm{solution}\:\mathrm{set}\:\mathrm{is}\:\left(−\mathrm{8};−\mathrm{7}\right)\cup\left(−\mathrm{2};−\mathrm{1}\right)\cup\left(\mathrm{4};\mathrm{5}\right)\cup\left(\mathrm{5};\mathrm{6}\right)\: \\ $$
Answered by bobhans last updated on 25/Feb/21
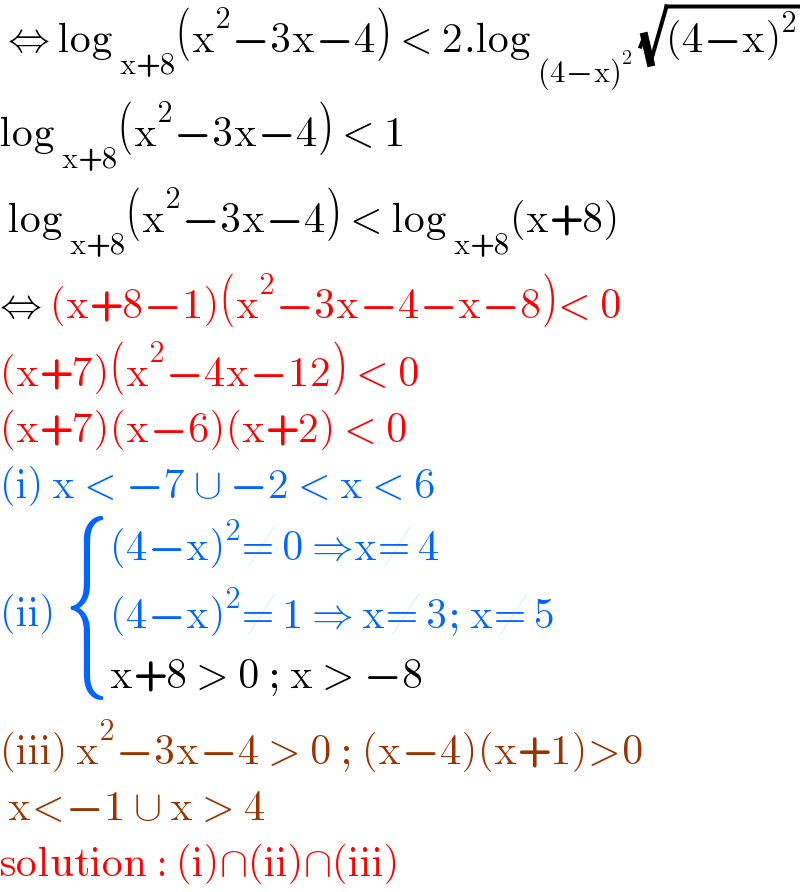
⇔ log _(x+8) (x^2 −3x−4) < 2.log _((4−x)^2 ) (√((4−x)^2 )) log _(x+8) (x^2 −3x−4) < 1 log _(x+8) (x^2 −3x−4) < log _(x+8) (x+8) ⇔ (x+8−1)(x^2 −3x−4−x−8)< 0 (x+7)(x^2 −4x−12) < 0 (x+7)(x−6)(x+2) < 0 (i) x < −7 ∪ −2 < x < 6 (ii) { (((4−x)^2 ≠ 0 ⇒x≠ 4)),(((4−x)^2 ≠ 1 ⇒ x≠ 3; x≠ 5)),((x+8 > 0 ; x > −8)) :} (iii) x^2 −3x−4 > 0 ; (x−4)(x+1)>0 x<−1 ∪ x > 4 solution : (i)∩(ii)∩(iii)
$$\:\Leftrightarrow\:\mathrm{log}\:_{\mathrm{x}+\mathrm{8}} \left(\mathrm{x}^{\mathrm{2}} −\mathrm{3x}−\mathrm{4}\right)\:<\:\mathrm{2}.\mathrm{log}\:_{\left(\mathrm{4}−\mathrm{x}\right)^{\mathrm{2}} } \:\sqrt{\left(\mathrm{4}−\mathrm{x}\right)^{\mathrm{2}} } \\ $$$$\mathrm{log}\:_{\mathrm{x}+\mathrm{8}} \left(\mathrm{x}^{\mathrm{2}} −\mathrm{3x}−\mathrm{4}\right)\:<\:\mathrm{1}\: \\ $$$$\:\mathrm{log}\:_{\mathrm{x}+\mathrm{8}} \left(\mathrm{x}^{\mathrm{2}} −\mathrm{3x}−\mathrm{4}\right)\:<\:\mathrm{log}\:_{\mathrm{x}+\mathrm{8}} \left(\mathrm{x}+\mathrm{8}\right) \\ $$$$\Leftrightarrow\:\left(\mathrm{x}+\mathrm{8}−\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{3x}−\mathrm{4}−\mathrm{x}−\mathrm{8}\right)<\:\mathrm{0} \\ $$$$\left(\mathrm{x}+\mathrm{7}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{4x}−\mathrm{12}\right)\:<\:\mathrm{0} \\ $$$$\left(\mathrm{x}+\mathrm{7}\right)\left(\mathrm{x}−\mathrm{6}\right)\left(\mathrm{x}+\mathrm{2}\right)\:<\:\mathrm{0} \\ $$$$\left(\mathrm{i}\right)\:\mathrm{x}\:<\:−\mathrm{7}\:\cup\:−\mathrm{2}\:<\:\mathrm{x}\:<\:\mathrm{6} \\ $$$$\left(\mathrm{ii}\right)\:\begin{cases}{\left(\mathrm{4}−\mathrm{x}\right)^{\mathrm{2}} \neq\:\mathrm{0}\:\Rightarrow\mathrm{x}\neq\:\mathrm{4}}\\{\left(\mathrm{4}−\mathrm{x}\right)^{\mathrm{2}} \neq\:\mathrm{1}\:\Rightarrow\:\mathrm{x}\neq\:\mathrm{3};\:\mathrm{x}\neq\:\mathrm{5}}\\{\mathrm{x}+\mathrm{8}\:>\:\mathrm{0}\:;\:\mathrm{x}\:>\:−\mathrm{8}}\end{cases} \\ $$$$\left(\mathrm{iii}\right)\:\mathrm{x}^{\mathrm{2}} −\mathrm{3x}−\mathrm{4}\:>\:\mathrm{0}\:;\:\left(\mathrm{x}−\mathrm{4}\right)\left(\mathrm{x}+\mathrm{1}\right)>\mathrm{0} \\ $$$$\:\mathrm{x}<−\mathrm{1}\:\cup\:\mathrm{x}\:>\:\mathrm{4}\: \\ $$$$\mathrm{solution}\::\:\left(\mathrm{i}\right)\cap\left(\mathrm{ii}\right)\cap\left(\mathrm{iii}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *