Question Number 5039 by Rasheed Soomro last updated on 05/Apr/16
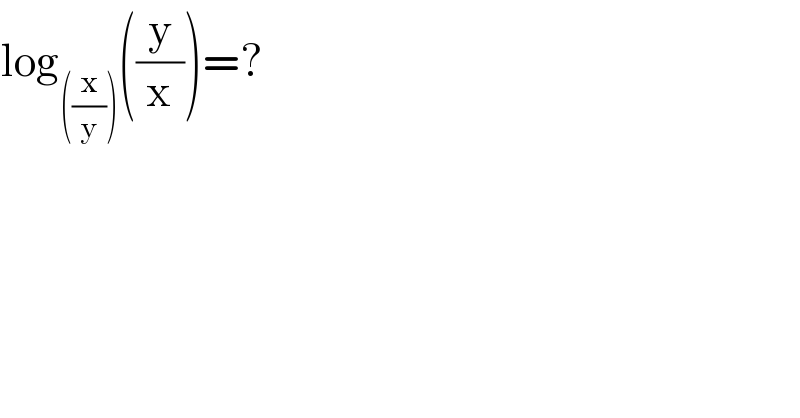
Answered by LMTV last updated on 05/Apr/16

Commented by FilupSmith last updated on 05/Apr/16
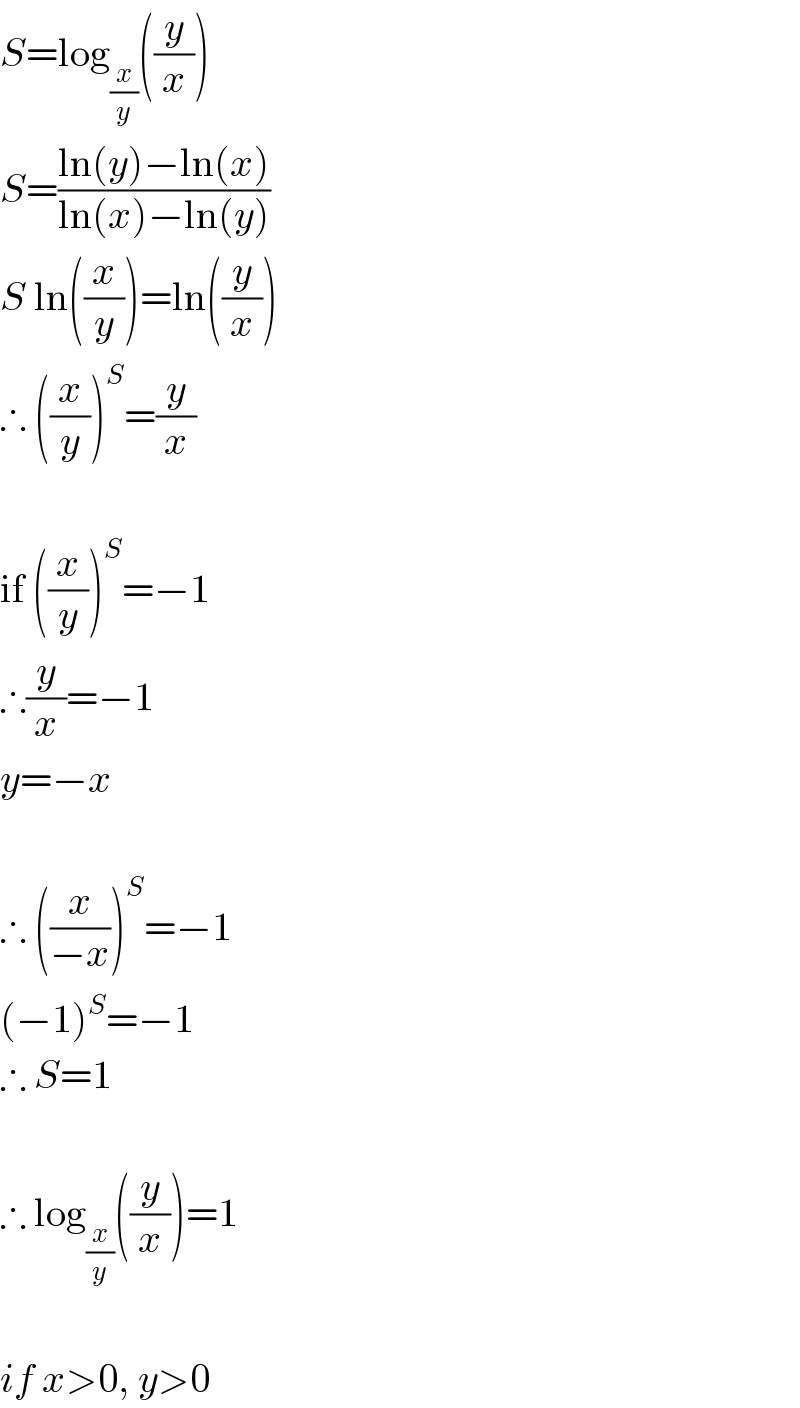
Commented by Rasheed Soomro last updated on 05/Apr/16
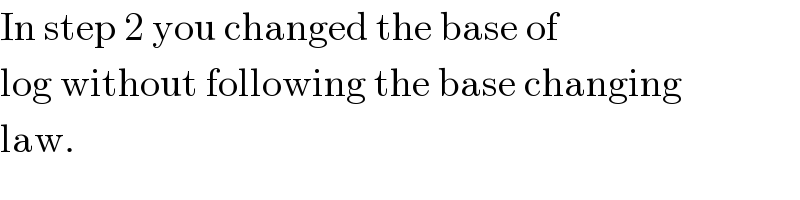
Commented by FilupSmith last updated on 06/Apr/16
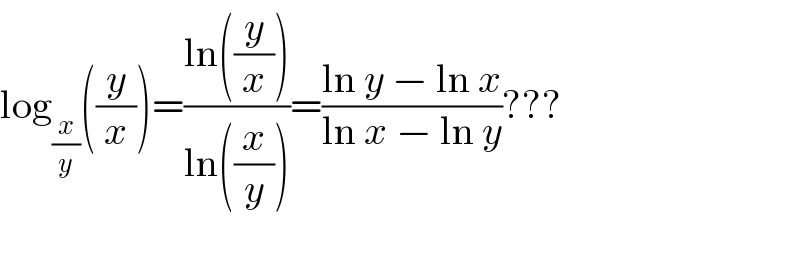
Commented by FilupSmith last updated on 06/Apr/16
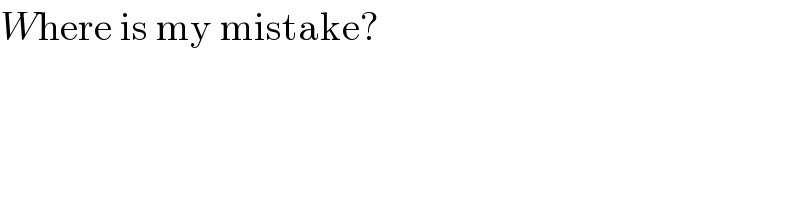
Commented by Rasheed Soomro last updated on 06/Apr/16
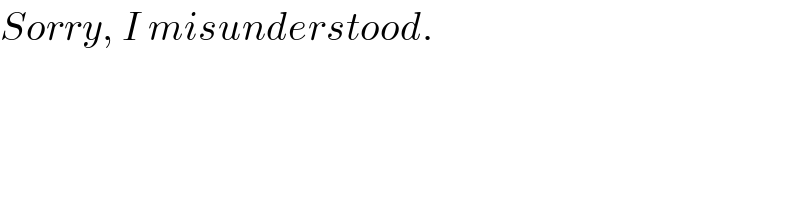
Answered by FilupSmith last updated on 05/Apr/16

Commented by FilupSmith last updated on 07/Apr/16

Commented by Rasheed Soomro last updated on 06/Apr/16
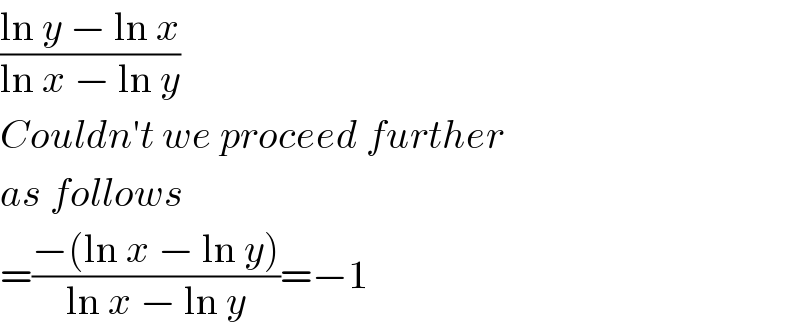
Answered by Rasheed Soomro last updated on 05/Apr/16
![log_(((x/y))) ((y/x))=? log_(((x/y))) ((x/y))^(−1) =(−1)log_(((x/y))) ((x/y))=(−1)(1)=−1 [∵log_a a=1]](https://www.tinkutara.com/question/Q5045.png)
