Menu Close

m-Z-x-2-m-1-x-m-2-16-0-f-x-1-f-x-2-0-x-1-lt-0-0-lt-x-2-m-

Tinku Tara 0 Comments
Pin




Question Number 11070 by ABD last updated on 10/Mar/17
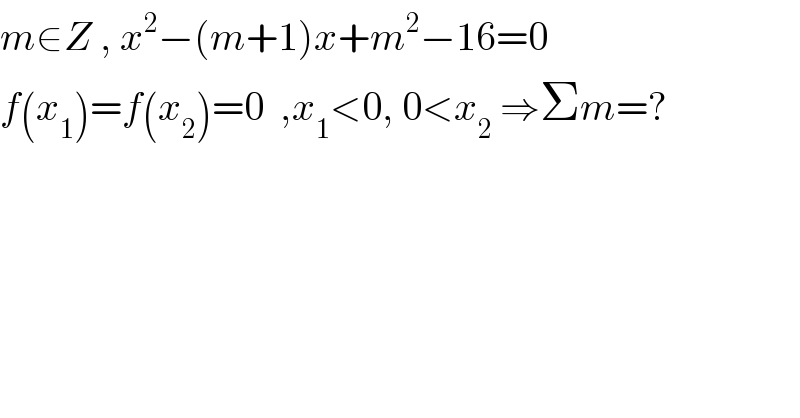
m∈Z , x^2 −(m+1)x+m^2 −16=0 f(x_1 )=f(x_2 )=0 ,x_1 <0, 0<x_2 ⇒Σm=?
$${m}\in{Z}\:,\:{x}^{\mathrm{2}} −\left({m}+\mathrm{1}\right){x}+{m}^{\mathrm{2}} −\mathrm{16}=\mathrm{0} \\ $$$${f}\left({x}_{\mathrm{1}} \right)={f}\left({x}_{\mathrm{2}} \right)=\mathrm{0}\:\:,{x}_{\mathrm{1}} <\mathrm{0},\:\mathrm{0}<{x}_{\mathrm{2}} \:\Rightarrow\Sigma{m}=? \\ $$
Answered by mrW1 last updated on 10/Mar/17
x=(((m+1)±(√((m+1)^2 −4(m^2 −16))))/2) x=(((m+1)±(√(m^2 +2m+1−4m^2 +64)))/2) x=(((1+m)±(√(65+2m−3m^2 )))/2) x=(((1+m)±(√(65+(1/3)−3(m^2 −2×(1/3)m+(1/9)))))/2) x=(((1+m)±(√(((196)/3)−3(m−(1/3))^2 )))/2) since x_1 and x_2 should be different, ((196)/3)−3(m−(1/3))^2 >0 (m−(1/3))^2 <((196)/9) ∣m−(1/3)∣<(√((196)/9))=((14)/3) −((14)/3)<m−(1/3)<((14)/3) m>−((14)/3)+(1/3)=−((13)/3) since m ∈Z, ⇒m≥−4 m<((14)/3)+(1/3)=((15)/3)=5 ⇒−4≤m≤4 ⇒Σm=0
$${x}=\frac{\left({m}+\mathrm{1}\right)\pm\sqrt{\left({m}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4}\left({m}^{\mathrm{2}} −\mathrm{16}\right)}}{\mathrm{2}} \\ $$$${x}=\frac{\left({m}+\mathrm{1}\right)\pm\sqrt{{m}^{\mathrm{2}} +\mathrm{2}{m}+\mathrm{1}−\mathrm{4}{m}^{\mathrm{2}} +\mathrm{64}}}{\mathrm{2}} \\ $$$${x}=\frac{\left(\mathrm{1}+{m}\right)\pm\sqrt{\mathrm{65}+\mathrm{2}{m}−\mathrm{3}{m}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$${x}=\frac{\left(\mathrm{1}+{m}\right)\pm\sqrt{\mathrm{65}+\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{3}\left({m}^{\mathrm{2}} −\mathrm{2}×\frac{\mathrm{1}}{\mathrm{3}}{m}+\frac{\mathrm{1}}{\mathrm{9}}\right)}}{\mathrm{2}} \\ $$$${x}=\frac{\left(\mathrm{1}+{m}\right)\pm\sqrt{\frac{\mathrm{196}}{\mathrm{3}}−\mathrm{3}\left({m}−\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} }}{\mathrm{2}} \\ $$$${since}\:{x}_{\mathrm{1}} \:{and}\:{x}_{\mathrm{2}} \:{should}\:{be}\:{different}, \\ $$$$\frac{\mathrm{196}}{\mathrm{3}}−\mathrm{3}\left({m}−\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} >\mathrm{0} \\ $$$$\left({m}−\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} <\frac{\mathrm{196}}{\mathrm{9}} \\ $$$$\mid{m}−\frac{\mathrm{1}}{\mathrm{3}}\mid<\sqrt{\frac{\mathrm{196}}{\mathrm{9}}}=\frac{\mathrm{14}}{\mathrm{3}} \\ $$$$−\frac{\mathrm{14}}{\mathrm{3}}<{m}−\frac{\mathrm{1}}{\mathrm{3}}<\frac{\mathrm{14}}{\mathrm{3}} \\ $$$${m}>−\frac{\mathrm{14}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}}=−\frac{\mathrm{13}}{\mathrm{3}} \\ $$$${since}\:{m}\:\in\mathbb{Z}, \\ $$$$\Rightarrow{m}\geqslant−\mathrm{4} \\ $$$${m}<\frac{\mathrm{14}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{15}}{\mathrm{3}}=\mathrm{5} \\ $$$$\Rightarrow−\mathrm{4}\leqslant{m}\leqslant\mathrm{4} \\ $$$$ \\ $$$$\Rightarrow\Sigma{m}=\mathrm{0} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *