Question Number 139104 by I want to learn more last updated on 22/Apr/21

$$\mathrm{Make}\:\:\mathrm{r}\:\:\mathrm{subject}\:\mathrm{formula}:\:\:\:\:\:\mathrm{S}_{\mathrm{n}} \:\:=\:\:\:\frac{\mathrm{a}\left(\mathrm{1}\:\:\:−\:\:\:\mathrm{r}^{\mathrm{n}} \right)}{\mathrm{1}\:\:−\:\:\:\mathrm{r}} \\ $$
Commented by mr W last updated on 22/Apr/21

$${you}\:{can}'{t}!\:{there}\:{is}\:{no}\:{formula}\:{for} \\ $$$${the}\:{roots}\:{of}\:{n}^{{th}} \:{degree}\:{polynomial} \\ $$$${equation}. \\ $$
Commented by I want to learn more last updated on 22/Apr/21
$$\mathrm{Thanks}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{appreciate} \\ $$
Commented by I want to learn more last updated on 23/Apr/21
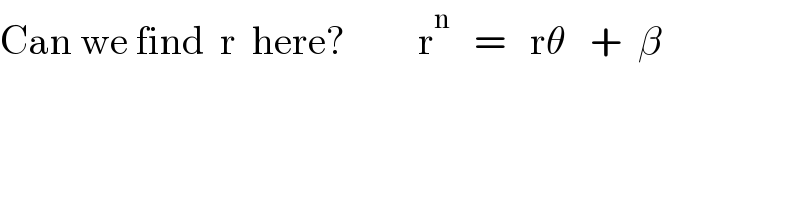
$$\mathrm{Can}\:\mathrm{we}\:\mathrm{find}\:\:\mathrm{r}\:\:\mathrm{here}?\:\:\:\:\:\:\:\:\:\mathrm{r}^{\mathrm{n}} \:\:\:=\:\:\:\mathrm{r}\theta\:\:\:+\:\:\beta \\ $$
Commented by MJS_new last updated on 23/Apr/21
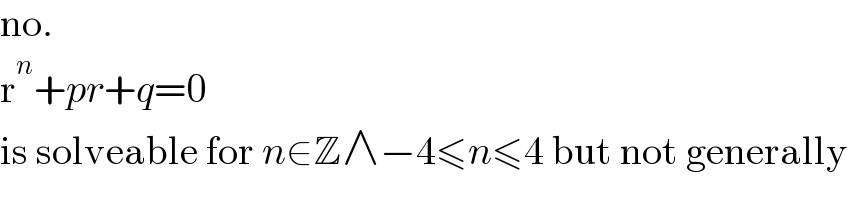
$$\mathrm{no}. \\ $$$$\mathrm{r}^{{n}} +{pr}+{q}=\mathrm{0} \\ $$$$\mathrm{is}\:\mathrm{solveable}\:\mathrm{for}\:{n}\in\mathbb{Z}\wedge−\mathrm{4}\leqslant{n}\leqslant\mathrm{4}\:\mathrm{but}\:\mathrm{not}\:\mathrm{generally} \\ $$
Answered by MJS_new last updated on 22/Apr/21
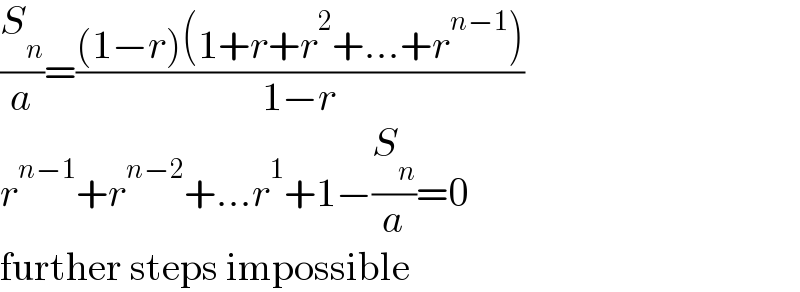
$$\frac{{S}_{{n}} }{{a}}=\frac{\left(\mathrm{1}−{r}\right)\left(\mathrm{1}+{r}+{r}^{\mathrm{2}} +…+{r}^{{n}−\mathrm{1}} \right)}{\mathrm{1}−{r}} \\ $$$${r}^{{n}−\mathrm{1}} +{r}^{{n}−\mathrm{2}} +…{r}^{\mathrm{1}} +\mathrm{1}−\frac{{S}_{{n}} }{{a}}=\mathrm{0} \\ $$$$\mathrm{further}\:\mathrm{steps}\:\mathrm{impossible} \\ $$
Commented by I want to learn more last updated on 23/Apr/21

$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$
