Question Number 139789 by mnjuly1970 last updated on 01/May/21

$$\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:……\mathscr{M}{athematical}\:…\:…\:…\:\mathscr{A}{nalysis}……. \\ $$$$\:\:\:\:{evaluation}\:::\:\mathscr{F}\::=\int_{\mathrm{0}} ^{\:\infty} {e}^{\frac{−\mathrm{2}}{{x}}} {sin}^{\mathrm{2}} \left(\frac{\mathrm{2}}{{x}}\right){dx}=? \\ $$$$ \\ $$$$\:\:\:\: \\ $$
Answered by Dwaipayan Shikari last updated on 01/May/21
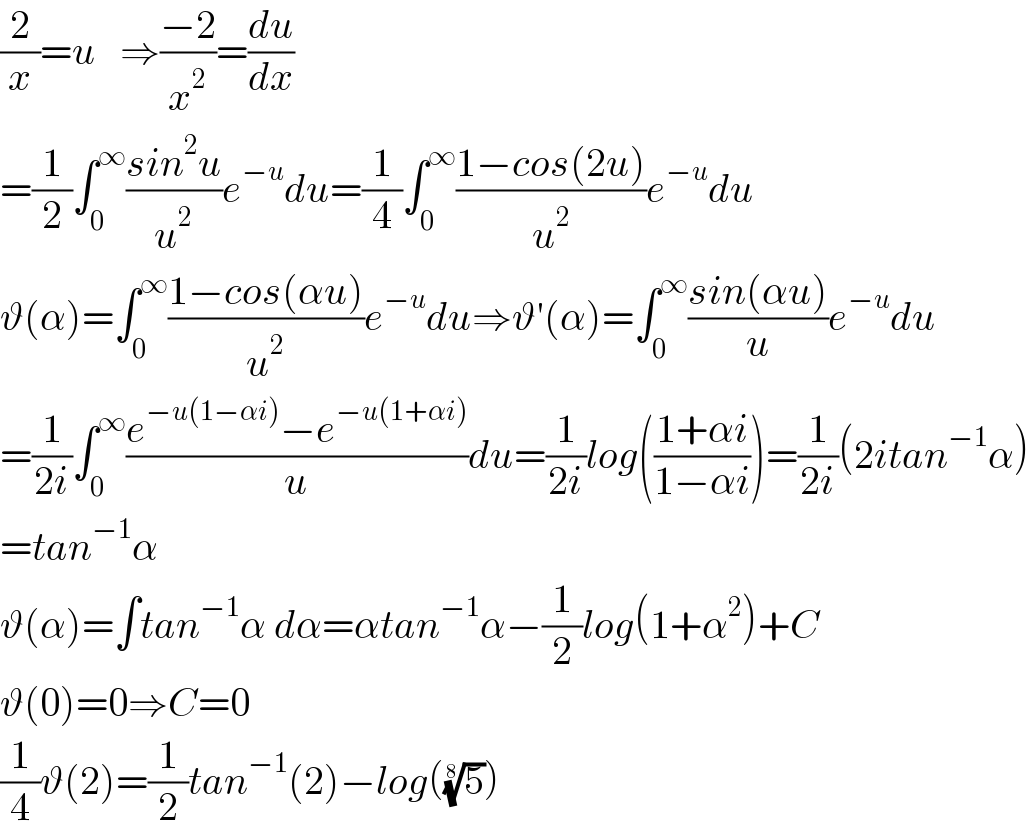
$$\frac{\mathrm{2}}{{x}}={u}\:\:\:\Rightarrow\frac{−\mathrm{2}}{{x}^{\mathrm{2}} }=\frac{{du}}{{dx}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{{sin}^{\mathrm{2}} {u}}{{u}^{\mathrm{2}} }{e}^{−{u}} {du}=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}−{cos}\left(\mathrm{2}{u}\right)}{{u}^{\mathrm{2}} }{e}^{−{u}} {du} \\ $$$$\vartheta\left(\alpha\right)=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}−{cos}\left(\alpha{u}\right)}{{u}^{\mathrm{2}} }{e}^{−{u}} {du}\Rightarrow\vartheta'\left(\alpha\right)=\int_{\mathrm{0}} ^{\infty} \frac{{sin}\left(\alpha{u}\right)}{{u}}{e}^{−{u}} {du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}}\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{u}\left(\mathrm{1}−\alpha{i}\right)} −{e}^{−{u}\left(\mathrm{1}+\alpha{i}\right)} }{{u}}{du}=\frac{\mathrm{1}}{\mathrm{2}{i}}{log}\left(\frac{\mathrm{1}+\alpha{i}}{\mathrm{1}−\alpha{i}}\right)=\frac{\mathrm{1}}{\mathrm{2}{i}}\left(\mathrm{2}{itan}^{−\mathrm{1}} \alpha\right) \\ $$$$={tan}^{−\mathrm{1}} \alpha \\ $$$$\vartheta\left(\alpha\right)=\int{tan}^{−\mathrm{1}} \alpha\:{d}\alpha=\alpha{tan}^{−\mathrm{1}} \alpha−\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)+{C} \\ $$$$\vartheta\left(\mathrm{0}\right)=\mathrm{0}\Rightarrow{C}=\mathrm{0}\:\: \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\vartheta\left(\mathrm{2}\right)=\frac{\mathrm{1}}{\mathrm{2}}{tan}^{−\mathrm{1}} \left(\mathrm{2}\right)−{log}\left(\sqrt[{\mathrm{8}}]{\mathrm{5}}\right) \\ $$
Commented by mnjuly1970 last updated on 01/May/21

$${mercey}\:{mr}\:{payan}… \\ $$
Answered by mathmax by abdo last updated on 01/May/21
![Φ=∫_0 ^∞ e^(−(2/x)) sin^2 ((2/x))dx ⇒Φ=_((2/x)=t→x=(2/t)) −∫_0 ^∞ e^(−t) sin^2 (t)(−(2/t^2 ))dt =2∫_0 ^∞ e^(−t) ((sin^2 t)/t^2 )dt =2 ∫_0 ^∞ e^(−t) .((1−cos(2t))/t^2 )dt let f(a)=∫_0 ^∞ ((1−cos(2t))/t^2 ) e^(−at) dt (a>0) ⇒ f^′ (a)=−∫_0 ^∞ (((1−cos(2t))e^(−at) )/t)dt and f^((2)) (a) =∫_0 ^∞ (1−cos(2t))e^(−at ) dt =∫_0 ^∞ e^(−at) dt −∫_0 ^∞ e^(−at) cos(2t)dt =[−(1/a)e^(−at) ]_0 ^∞ −Re(∫_0 ^∞ e^(−at+2it) dt) ∫_0 ^∞ e^((−a+2i)t) dt =[(1/(−a+2i))e^((−a+2i)t) ]_0 ^∞ =−(1/(−a+2i)) =(1/(a−2i)) =((a+2i)/(a^2 +4)) ⇒f^((2)) (a)=(1/a)−(a/(a^2 +4)) ⇒ f^′ (a) =lna−(1/2)ln(a^2 +4) +c (c=0) ⇒ f(a) =alna−a −(1/2)∫ ln(a^2 +4)da +c ∫ ln(a^2 +4)da =alna−∫ a.((2a)/(a^2 +4))da =alna−2∫ ((a^2 +4−4)/(a^2 +4))da =alna−2a +8∫ (da/(a^2 +4))(a=2u) =alna−2a +8∫ ((2du)/(4(1+u^2 ))) =alna−2a+4arctan((a/2)) ⇒ f(a)=alna−a−(1/2)alna+a−2arctan((a/2)) +c f(1)=c−2 arctan((1/2)) and Φ=2f(1)=2c−4arctan((1/2)) rest to calculate c....be continued....](https://www.tinkutara.com/question/Q139828.png)
$$\Phi=\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{e}^{−\frac{\mathrm{2}}{\mathrm{x}}} \:\mathrm{sin}^{\mathrm{2}} \left(\frac{\mathrm{2}}{\mathrm{x}}\right)\mathrm{dx}\:\Rightarrow\Phi=_{\frac{\mathrm{2}}{\mathrm{x}}=\mathrm{t}\rightarrow\mathrm{x}=\frac{\mathrm{2}}{\mathrm{t}}} \:\:\:\:−\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{t}} \:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{t}\right)\left(−\frac{\mathrm{2}}{\mathrm{t}^{\mathrm{2}} }\right)\mathrm{dt} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{e}^{−\mathrm{t}} \:\frac{\mathrm{sin}^{\mathrm{2}} \mathrm{t}}{\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{t}} .\frac{\mathrm{1}−\mathrm{cos}\left(\mathrm{2t}\right)}{\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:\:\mathrm{let} \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}−\mathrm{cos}\left(\mathrm{2t}\right)}{\mathrm{t}^{\mathrm{2}} }\:\mathrm{e}^{−\mathrm{at}} \:\mathrm{dt}\:\:\:\left(\mathrm{a}>\mathrm{0}\right)\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)=−\int_{\mathrm{0}} ^{\infty} \:\:\frac{\left(\mathrm{1}−\mathrm{cos}\left(\mathrm{2t}\right)\right)\mathrm{e}^{−\mathrm{at}} }{\mathrm{t}}\mathrm{dt}\:\mathrm{and} \\ $$$$\mathrm{f}^{\left(\mathrm{2}\right)} \left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\left(\mathrm{1}−\mathrm{cos}\left(\mathrm{2t}\right)\right)\mathrm{e}^{−\mathrm{at}\:} \mathrm{dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{at}} \:\mathrm{dt}\:−\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{at}} \:\mathrm{cos}\left(\mathrm{2t}\right)\mathrm{dt} \\ $$$$=\left[−\frac{\mathrm{1}}{\mathrm{a}}\mathrm{e}^{−\mathrm{at}} \right]_{\mathrm{0}} ^{\infty} −\mathrm{Re}\left(\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{at}+\mathrm{2it}} \mathrm{dt}\right) \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{\left(−\mathrm{a}+\mathrm{2i}\right)\mathrm{t}} \:\mathrm{dt}\:=\left[\frac{\mathrm{1}}{−\mathrm{a}+\mathrm{2i}}\mathrm{e}^{\left(−\mathrm{a}+\mathrm{2i}\right)\mathrm{t}} \right]_{\mathrm{0}} ^{\infty} \\ $$$$=−\frac{\mathrm{1}}{−\mathrm{a}+\mathrm{2i}}\:=\frac{\mathrm{1}}{\mathrm{a}−\mathrm{2i}}\:=\frac{\mathrm{a}+\mathrm{2i}}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{4}}\:\Rightarrow\mathrm{f}^{\left(\mathrm{2}\right)} \left(\mathrm{a}\right)=\frac{\mathrm{1}}{\mathrm{a}}−\frac{\mathrm{a}}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{4}}\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)\:=\mathrm{lna}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{a}^{\mathrm{2}} \:+\mathrm{4}\right)\:+\mathrm{c}\:\left(\mathrm{c}=\mathrm{0}\right)\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{a}\right)\:=\mathrm{alna}−\mathrm{a}\:−\frac{\mathrm{1}}{\mathrm{2}}\int\:\mathrm{ln}\left(\mathrm{a}^{\mathrm{2}} \:+\mathrm{4}\right)\mathrm{da}\:+\mathrm{c} \\ $$$$\int\:\mathrm{ln}\left(\mathrm{a}^{\mathrm{2}} \:+\mathrm{4}\right)\mathrm{da}\:=\mathrm{alna}−\int\:\mathrm{a}.\frac{\mathrm{2a}}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{4}}\mathrm{da} \\ $$$$=\mathrm{alna}−\mathrm{2}\int\:\frac{\mathrm{a}^{\mathrm{2}} +\mathrm{4}−\mathrm{4}}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{4}}\mathrm{da}\:=\mathrm{alna}−\mathrm{2a}\:+\mathrm{8}\int\:\frac{\mathrm{da}}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{4}}\left(\mathrm{a}=\mathrm{2u}\right) \\ $$$$=\mathrm{alna}−\mathrm{2a}\:+\mathrm{8}\int\:\:\frac{\mathrm{2du}}{\mathrm{4}\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)}\:=\mathrm{alna}−\mathrm{2a}+\mathrm{4arctan}\left(\frac{\mathrm{a}}{\mathrm{2}}\right)\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=\mathrm{alna}−\mathrm{a}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{alna}+\mathrm{a}−\mathrm{2arctan}\left(\frac{\mathrm{a}}{\mathrm{2}}\right)\:+\mathrm{c}\:\: \\ $$$$\mathrm{f}\left(\mathrm{1}\right)=\mathrm{c}−\mathrm{2}\:\mathrm{arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:\mathrm{and}\:\Phi=\mathrm{2f}\left(\mathrm{1}\right)=\mathrm{2c}−\mathrm{4arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\mathrm{rest}\:\mathrm{to}\:\mathrm{calculate}\:\mathrm{c}….\mathrm{be}\:\mathrm{continued}…. \\ $$
