Question Number 136448 by adhigenz last updated on 22/Mar/21

$$\mathrm{Mr}.\mathrm{A}\:\mathrm{wants}\:\mathrm{to}\:\mathrm{deliver}\:\mathrm{7}\:\mathrm{letters}\:\mathrm{to}\:\mathrm{his}\:\mathrm{7}\:\mathrm{friends}\:\mathrm{so}\:\mathrm{that}\:\mathrm{each}\:\mathrm{gets}\:\mathrm{1}\:\mathrm{letter}. \\ $$$$\mathrm{All}\:\mathrm{of}\:\mathrm{the}\:\mathrm{letters}\:\mathrm{are}\:\mathrm{written}\:\mathrm{of}\:\mathrm{the}\:\mathrm{addresses}\:\mathrm{of}\:\mathrm{his}\:\mathrm{7}\:\mathrm{friends}.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{probbility}\:\mathrm{that}, \\ $$$$\mathrm{3}\:\mathrm{of}\:\mathrm{his}\:\mathrm{friends}\:\mathrm{receive}\:\mathrm{the}\:\mathrm{correct}\:\mathrm{letters}\:\mathrm{and}\:\mathrm{the}\:\mathrm{remaining}\:\mathrm{4}\:\mathrm{receive}\:\mathrm{the}\:\mathrm{wrong}\:\mathrm{ones}. \\ $$
Answered by mr W last updated on 22/Mar/21
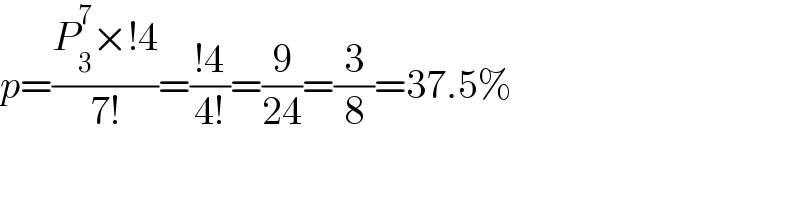
$${p}=\frac{{P}_{\mathrm{3}} ^{\mathrm{7}} ×!\mathrm{4}}{\mathrm{7}!}=\frac{!\mathrm{4}}{\mathrm{4}!}=\frac{\mathrm{9}}{\mathrm{24}}=\frac{\mathrm{3}}{\mathrm{8}}=\mathrm{37}.\mathrm{5\%} \\ $$
Commented by john_santu last updated on 23/Mar/21

$${i}\:{think}\:{it}\:\frac{\mathrm{1}}{\mathrm{16}}\:{sir} \\ $$
Commented by john_santu last updated on 23/Mar/21
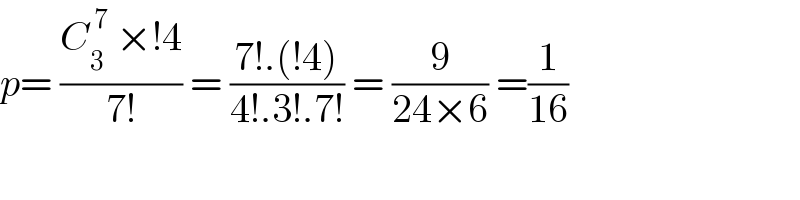
$${p}=\:\frac{{C}_{\mathrm{3}} ^{\:\mathrm{7}} \:×!\mathrm{4}}{\mathrm{7}!}\:=\:\frac{\mathrm{7}!.\left(!\mathrm{4}\right)}{\mathrm{4}!.\mathrm{3}!.\mathrm{7}!}\:=\:\frac{\mathrm{9}}{\mathrm{24}×\mathrm{6}}\:=\frac{\mathrm{1}}{\mathrm{16}} \\ $$
Commented by mr W last updated on 23/Mar/21

$${yes}! \\ $$
