Question Number 142148 by islamo last updated on 27/May/21

$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{{n}!}=? \\ $$
Answered by mathmax by abdo last updated on 27/May/21
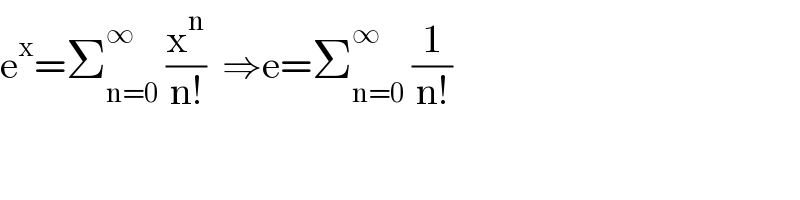
$$\mathrm{e}^{\mathrm{x}} =\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}!}\:\:\Rightarrow\mathrm{e}=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}!} \\ $$
