Menu Close

n-0-2n-2-1-n-4-n-

Tinku Tara 0 Comments
Pin




Question Number 142349 by mnjuly1970 last updated on 30/May/21
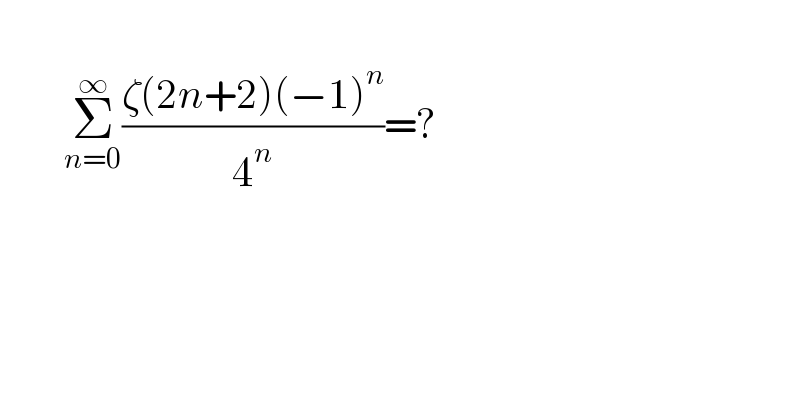
Σ_(n=0) ^∞ ((ζ(2n+2)(−1)^n )/4^n )=?
$$ \\ $$$$\:\:\:\:\:\:\:\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\zeta\left(\mathrm{2}{n}+\mathrm{2}\right)\left(−\mathrm{1}\right)^{{n}} }{\mathrm{4}^{{n}} }=? \\ $$
Answered by Dwaipayan Shikari last updated on 30/May/21
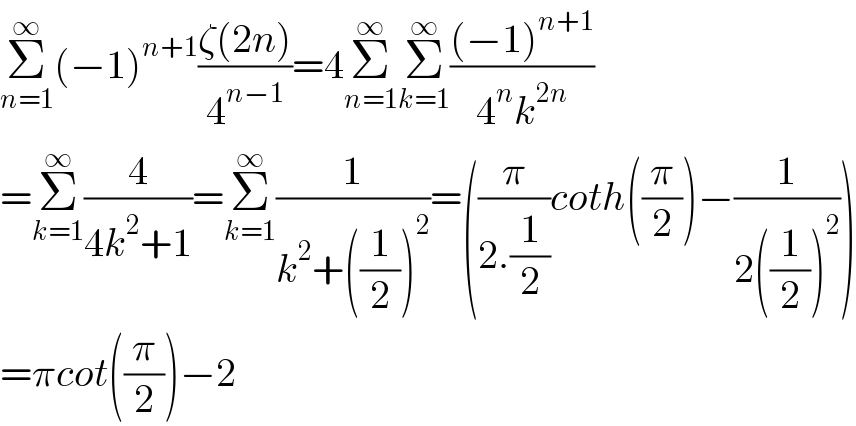
Σ_(n=1) ^∞ (−1)^(n+1) ((ζ(2n))/4^(n−1) )=4Σ_(n=1) ^∞ Σ_(k=1) ^∞ (((−1)^(n+1) )/(4^n k^(2n) )) =Σ_(k=1) ^∞ (4/(4k^2 +1))=Σ_(k=1) ^∞ (1/(k^2 +((1/2))^2 ))=((π/(2.(1/2)))coth((π/2))−(1/(2((1/2))^2 ))) =πcot((π/2))−2
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \frac{\zeta\left(\mathrm{2}{n}\right)}{\mathrm{4}^{{n}−\mathrm{1}} }=\mathrm{4}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\mathrm{4}^{{n}} {k}^{\mathrm{2}{n}} } \\ $$$$=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{4}}{\mathrm{4}{k}^{\mathrm{2}} +\mathrm{1}}=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }=\left(\frac{\pi}{\mathrm{2}.\frac{\mathrm{1}}{\mathrm{2}}}{coth}\left(\frac{\pi}{\mathrm{2}}\right)−\frac{\mathrm{1}}{\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }\right) \\ $$$$=\pi{cot}\left(\frac{\pi}{\mathrm{2}}\right)−\mathrm{2} \\ $$
Commented by mnjuly1970 last updated on 30/May/21
thank you so much..
$$\:\:{thank}\:{you}\:{so}\:{much}.. \\ $$
Answered by mnjuly1970 last updated on 30/May/21
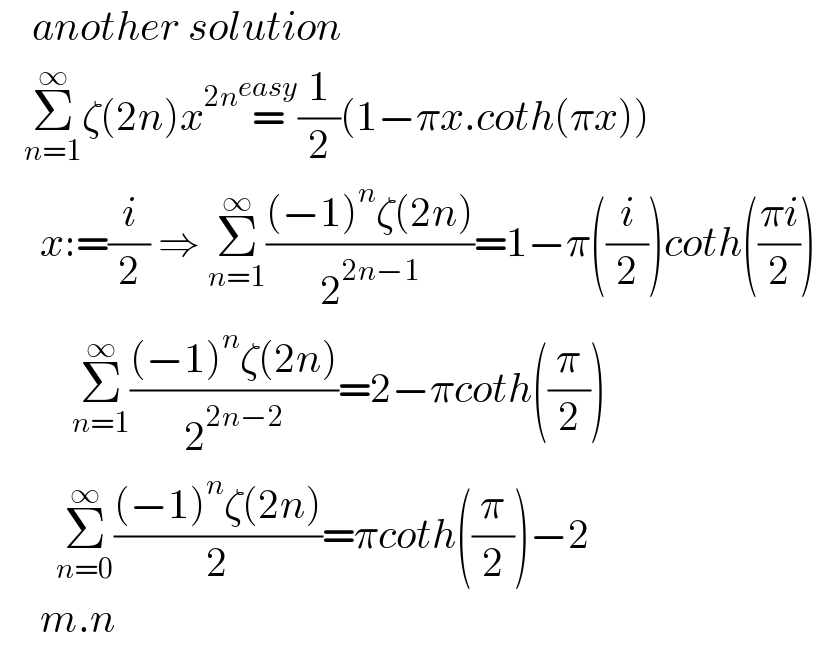
another solution Σ_(n=1) ^∞ ζ(2n)x^(2n) =^(easy) (1/2)(1−πx.coth(πx)) x:=(i/2) ⇒ Σ_(n=1) ^∞ (((−1)^n ζ(2n))/2^(2n−1) )=1−π((i/2))coth(((πi)/2)) Σ_(n=1) ^∞ (((−1)^n ζ(2n))/2^(2n−2) )=2−πcoth((π/2)) Σ_(n=0) ^∞ (((−1)^n ζ(2n))/2)=πcoth((π/2))−2 m.n
$$\:\:\:\:{another}\:{solution} \\ $$$$\:\:\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\zeta\left(\mathrm{2}{n}\right){x}^{\mathrm{2}{n}} \overset{{easy}} {=}\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\pi{x}.{coth}\left(\pi{x}\right)\right) \\ $$$$\:\:\:\:\:{x}:=\frac{{i}}{\mathrm{2}}\:\Rightarrow\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} \zeta\left(\mathrm{2}{n}\right)}{\mathrm{2}^{\mathrm{2}{n}−\mathrm{1}} }=\mathrm{1}−\pi\left(\frac{{i}}{\mathrm{2}}\right){coth}\left(\frac{\pi{i}}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} \zeta\left(\mathrm{2}{n}\right)}{\mathrm{2}^{\mathrm{2}{n}−\mathrm{2}} }=\mathrm{2}−\pi{coth}\left(\frac{\pi}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} \zeta\left(\mathrm{2}{n}\right)}{\mathrm{2}}=\pi{coth}\left(\frac{\pi}{\mathrm{2}}\right)−\mathrm{2} \\ $$$$\:\:\:\:\:{m}.{n} \\ $$
Commented by Dwaipayan Shikari last updated on 30/May/21
Nice sir!
$${Nice}\:{sir}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *