Menu Close

n-0-4n-2n-1-16-15-3-27-pi-2-5-25-ln-1-5-2-

Tinku Tara 0 Comments
Pin




Question Number 137936 by Ñï= last updated on 08/Apr/21
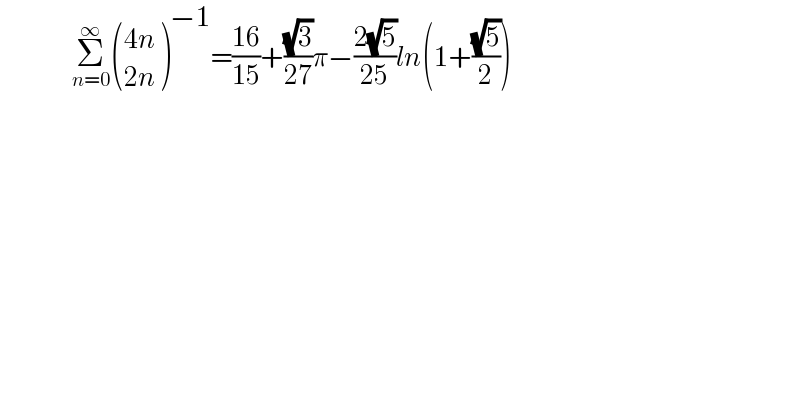
Σ_(n=0) ^∞ (((4n)),((2n)) )^(−1) =((16)/(15))+((√3)/(27))π−((2(√5))/(25))ln(1+((√5)/2))
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\begin{pmatrix}{\mathrm{4}{n}}\\{\mathrm{2}{n}}\end{pmatrix}^{−\mathrm{1}} =\frac{\mathrm{16}}{\mathrm{15}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{27}}\pi−\frac{\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{25}}{ln}\left(\mathrm{1}+\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right) \\ $$
Commented by Dwaipayan Shikari last updated on 08/Apr/21
Σ_(n=0) ^∞ (1/ (((4n)),((2n)) ))=Σ_(n=0) ^∞ ((Γ^2 (2n+1))/(Γ(4n+1))) Γ(2n)=(2^(2n−1) /( (√π)))Γ(n+(1/2))Γ(n) Γ(2(2n+(1/2)))=(2^(4n) /( (√π)))Γ(2n+1)Γ(2n+(1/2)) Γ(2n+1)=(2^(2n) /( (√π)))Γ(n+1)Γ(n+(1/2))⇒Γ^2 (2n+1)=(2^(4n) /π)Γ^2 (n+1)Γ^2 (n+(1/2)) Γ(2n+(1/2))=(2^(2n−(1/2)) /( (√π)))Γ(n+(1/4))Γ(n+(3/4)) Γ(4n+1)=(2^(8n−(1/2)) /π^(3/2) )Γ(n+(1/2))Γ(n+(1/4))Γ(n+(3/4))Γ(n+1) Σ_(n=0) ^∞ ((Γ^2 (2n+1))/(Γ(4n+1)))=Σ_(n=0) ^∞ (((√(2π)) Γ(n+1)Γ(n+(1/2)))/(Γ(n+(1/4))Γ(n+(3/4)))).(1/2^(4n) ) =(√(2π)).((√π)/( (√2)π))Σ_(n=0) ^∞ (((1)_n ((1/2))_n )/(((1/4))_n ((3/4))_n )).(1/(16^n ))= _2 F_2 (1,(1/2);(1/4);(3/4);(1/(16)))
$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\begin{pmatrix}{\mathrm{4}{n}}\\{\mathrm{2}{n}}\end{pmatrix}}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\Gamma^{\mathrm{2}} \left(\mathrm{2}{n}+\mathrm{1}\right)}{\Gamma\left(\mathrm{4}{n}+\mathrm{1}\right)} \\ $$$$\Gamma\left(\mathrm{2}{n}\right)=\frac{\mathrm{2}^{\mathrm{2}{n}−\mathrm{1}} }{\:\sqrt{\pi}}\Gamma\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left({n}\right) \\ $$$$\Gamma\left(\mathrm{2}\left(\mathrm{2}{n}+\frac{\mathrm{1}}{\mathrm{2}}\right)\right)=\frac{\mathrm{2}^{\mathrm{4}{n}} }{\:\sqrt{\pi}}\Gamma\left(\mathrm{2}{n}+\mathrm{1}\right)\Gamma\left(\mathrm{2}{n}+\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\Gamma\left(\mathrm{2}{n}+\mathrm{1}\right)=\frac{\mathrm{2}^{\mathrm{2}{n}} }{\:\sqrt{\pi}}\Gamma\left({n}+\mathrm{1}\right)\Gamma\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)\Rightarrow\Gamma^{\mathrm{2}} \left(\mathrm{2}{n}+\mathrm{1}\right)=\frac{\mathrm{2}^{\mathrm{4}{n}} }{\pi}\Gamma^{\mathrm{2}} \left({n}+\mathrm{1}\right)\Gamma^{\mathrm{2}} \left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\Gamma\left(\mathrm{2}{n}+\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\mathrm{2}^{\mathrm{2}{n}−\frac{\mathrm{1}}{\mathrm{2}}} }{\:\sqrt{\pi}}\Gamma\left({n}+\frac{\mathrm{1}}{\mathrm{4}}\right)\Gamma\left({n}+\frac{\mathrm{3}}{\mathrm{4}}\right) \\ $$$$\Gamma\left(\mathrm{4}{n}+\mathrm{1}\right)=\frac{\mathrm{2}^{\mathrm{8}{n}−\frac{\mathrm{1}}{\mathrm{2}}} }{\pi^{\mathrm{3}/\mathrm{2}} }\Gamma\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left({n}+\frac{\mathrm{1}}{\mathrm{4}}\right)\Gamma\left({n}+\frac{\mathrm{3}}{\mathrm{4}}\right)\Gamma\left({n}+\mathrm{1}\right) \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\Gamma^{\mathrm{2}} \left(\mathrm{2}{n}+\mathrm{1}\right)}{\Gamma\left(\mathrm{4}{n}+\mathrm{1}\right)}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\sqrt{\mathrm{2}\pi}\:\Gamma\left({n}+\mathrm{1}\right)\Gamma\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left({n}+\frac{\mathrm{1}}{\mathrm{4}}\right)\Gamma\left({n}+\frac{\mathrm{3}}{\mathrm{4}}\right)}.\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{4}{n}} } \\ $$$$=\sqrt{\mathrm{2}\pi}.\frac{\sqrt{\pi}}{\:\sqrt{\mathrm{2}}\pi}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\mathrm{1}\right)_{{n}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)_{{n}} }{\left(\frac{\mathrm{1}}{\mathrm{4}}\right)_{{n}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)_{{n}} }.\frac{\mathrm{1}}{\mathrm{16}^{{n}} }=\:_{\mathrm{2}} {F}_{\mathrm{2}} \left(\mathrm{1},\frac{\mathrm{1}}{\mathrm{2}};\frac{\mathrm{1}}{\mathrm{4}};\frac{\mathrm{3}}{\mathrm{4}};\frac{\mathrm{1}}{\mathrm{16}}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *