Question Number 142150 by iloveisrael last updated on 27/May/21
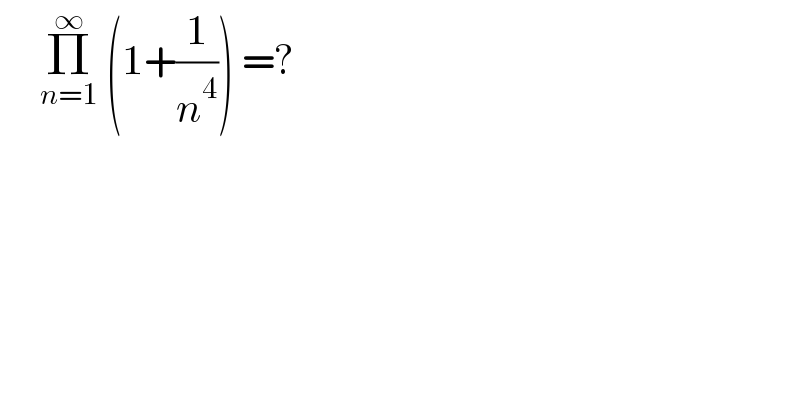
$$\:\:\:\:\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\:\left(\mathrm{1}+\frac{\mathrm{1}}{{n}^{\mathrm{4}} }\right)\:=?\: \\ $$
Commented by liberty last updated on 27/May/21
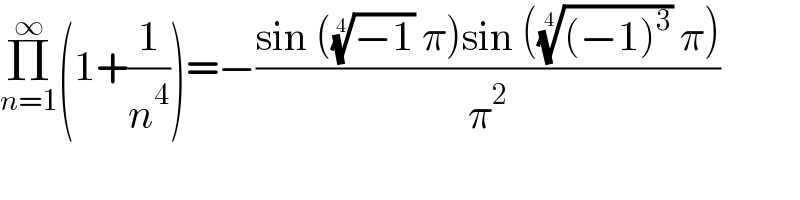
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}^{\mathrm{4}} }\right)=−\frac{\mathrm{sin}\:\left(\sqrt[{\mathrm{4}}]{−\mathrm{1}}\:\pi\right)\mathrm{sin}\:\left(\sqrt[{\mathrm{4}}]{\left(−\mathrm{1}\right)^{\mathrm{3}} }\:\pi\right)}{\pi^{\mathrm{2}} } \\ $$
Answered by Dwaipayan Shikari last updated on 27/May/21
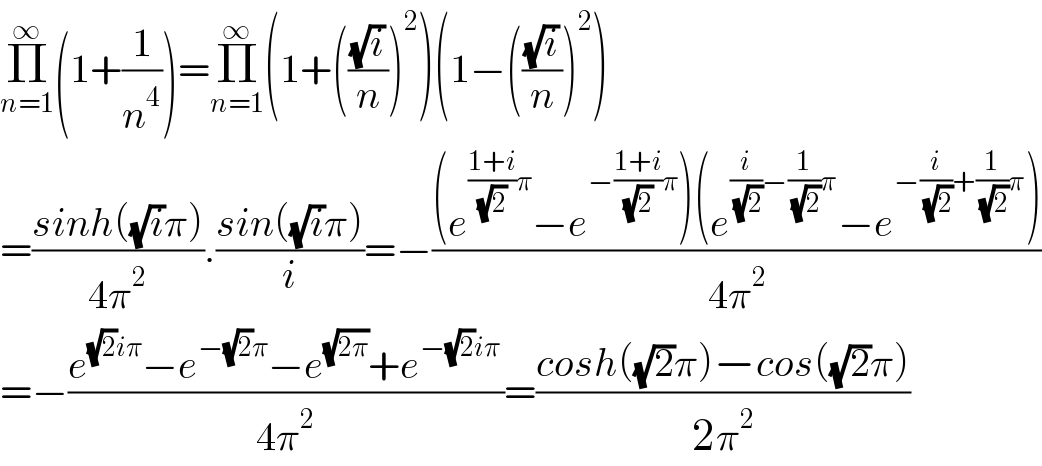
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}^{\mathrm{4}} }\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}+\left(\frac{\sqrt{{i}}}{{n}}\right)^{\mathrm{2}} \right)\left(\mathrm{1}−\left(\frac{\sqrt{{i}}}{{n}}\right)^{\mathrm{2}} \right) \\ $$$$=\frac{{sinh}\left(\sqrt{{i}}\pi\right)}{\mathrm{4}\pi^{\mathrm{2}} }.\frac{{sin}\left(\sqrt{{i}}\pi\right)}{{i}}=−\frac{\left({e}^{\frac{\mathrm{1}+{i}}{\:\sqrt{\mathrm{2}}}\pi} −{e}^{−\frac{\mathrm{1}+{i}}{\:\sqrt{\mathrm{2}}}\pi} \right)\left({e}^{\frac{{i}}{\:\sqrt{\mathrm{2}}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\pi} −{e}^{−\frac{{i}}{\:\sqrt{\mathrm{2}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\pi} \right)}{\mathrm{4}\pi^{\mathrm{2}} } \\ $$$$=−\frac{{e}^{\sqrt{\mathrm{2}}{i}\pi} −{e}^{−\sqrt{\mathrm{2}}\pi} −{e}^{\sqrt{\mathrm{2}\pi}} +{e}^{−\sqrt{\mathrm{2}}{i}\pi} }{\mathrm{4}\pi^{\mathrm{2}} }=\frac{{cosh}\left(\sqrt{\mathrm{2}}\pi\right)−{cos}\left(\sqrt{\mathrm{2}}\pi\right)}{\mathrm{2}\pi^{\mathrm{2}} } \\ $$
