Question Number 75828 by 21042004 last updated on 18/Dec/19

$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{10}^{{n}} } \\ $$
Commented by mathmax by abdo last updated on 18/Dec/19
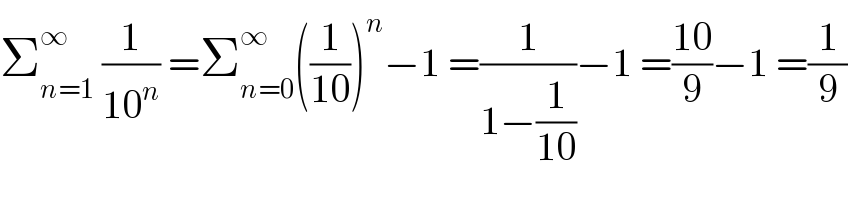
$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{10}^{{n}} }\:=\sum_{{n}=\mathrm{0}} ^{\infty} \left(\frac{\mathrm{1}}{\mathrm{10}}\right)^{{n}} −\mathrm{1}\:=\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{10}}}−\mathrm{1}\:=\frac{\mathrm{10}}{\mathrm{9}}−\mathrm{1}\:=\frac{\mathrm{1}}{\mathrm{9}} \\ $$
Answered by MJS last updated on 18/Dec/19
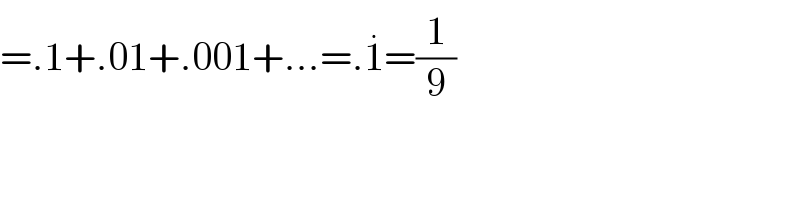
$$=.\mathrm{1}+.\mathrm{01}+.\mathrm{001}+…=.\overset{.} {\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{9}} \\ $$
