Question Number 133075 by LUFFY last updated on 18/Feb/21
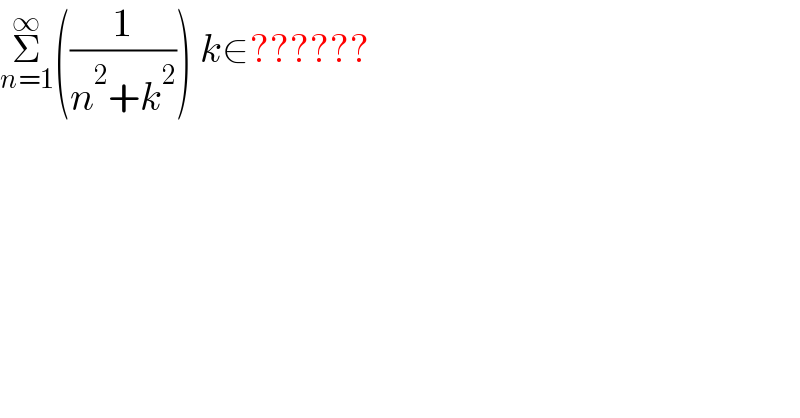
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}^{\mathrm{2}} +{k}^{\mathrm{2}} }\right)\:{k}\in?????? \\ $$
Answered by Dwaipayan Shikari last updated on 18/Feb/21
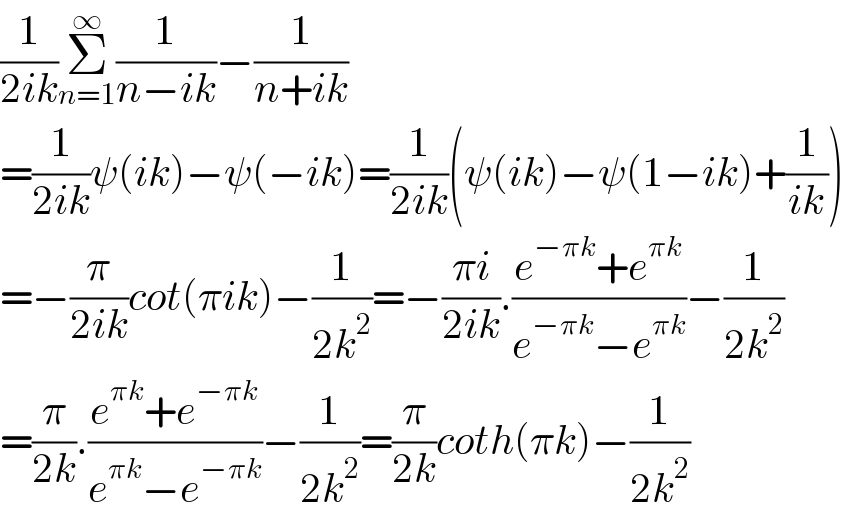
$$\frac{\mathrm{1}}{\mathrm{2}{ik}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}−{ik}}−\frac{\mathrm{1}}{{n}+{ik}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{ik}}\psi\left({ik}\right)−\psi\left(−{ik}\right)=\frac{\mathrm{1}}{\mathrm{2}{ik}}\left(\psi\left({ik}\right)−\psi\left(\mathrm{1}−{ik}\right)+\frac{\mathrm{1}}{{ik}}\right) \\ $$$$=−\frac{\pi}{\mathrm{2}{ik}}{cot}\left(\pi{ik}\right)−\frac{\mathrm{1}}{\mathrm{2}{k}^{\mathrm{2}} }=−\frac{\pi{i}}{\mathrm{2}{ik}}.\frac{{e}^{−\pi{k}} +{e}^{\pi{k}} }{{e}^{−\pi{k}} −{e}^{\pi{k}} }−\frac{\mathrm{1}}{\mathrm{2}{k}^{\mathrm{2}} } \\ $$$$=\frac{\pi}{\mathrm{2}{k}}.\frac{{e}^{\pi{k}} +{e}^{−\pi{k}} }{{e}^{\pi{k}} −{e}^{−\pi{k}} }−\frac{\mathrm{1}}{\mathrm{2}{k}^{\mathrm{2}} }=\frac{\pi}{\mathrm{2}{k}}{coth}\left(\pi{k}\right)−\frac{\mathrm{1}}{\mathrm{2}{k}^{\mathrm{2}} } \\ $$
Commented by LUFFY last updated on 19/Feb/21

$${k}\:{belongs}\:{to}\:??????? \\ $$
Commented by Dwaipayan Shikari last updated on 19/Feb/21
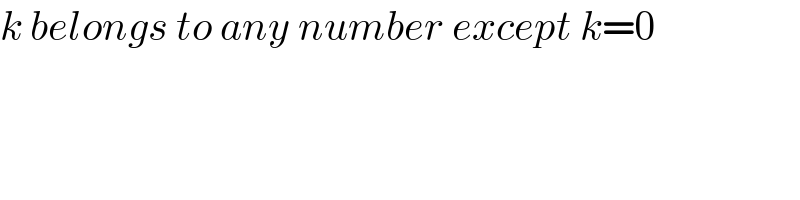
$${k}\:{belongs}\:{to}\:{any}\:{number}\:{except}\:{k}=\mathrm{0} \\ $$
