Question Number 131877 by Dwaipayan Shikari last updated on 09/Feb/21

$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}\left({e}^{\mathrm{2}\pi{n}} −\mathrm{1}\right)} \\ $$
Commented by Dwaipayan Shikari last updated on 09/Feb/21
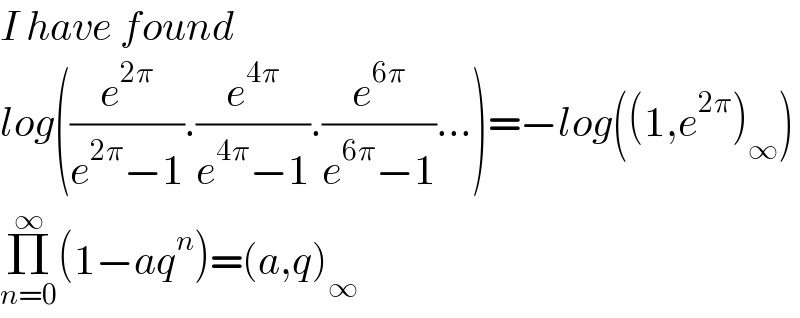
$${I}\:{have}\:{found}\: \\ $$$${log}\left(\frac{{e}^{\mathrm{2}\pi} }{{e}^{\mathrm{2}\pi} −\mathrm{1}}.\frac{{e}^{\mathrm{4}\pi} }{{e}^{\mathrm{4}\pi} −\mathrm{1}}.\frac{{e}^{\mathrm{6}\pi} }{{e}^{\mathrm{6}\pi} −\mathrm{1}}…\right)=−{log}\left(\left(\mathrm{1},{e}^{\mathrm{2}\pi} \right)_{\infty} \right) \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\prod}}\left(\mathrm{1}−{aq}^{{n}} \right)=\left({a},{q}\right)_{\infty} \:\: \\ $$
Commented by SEKRET last updated on 09/Feb/21
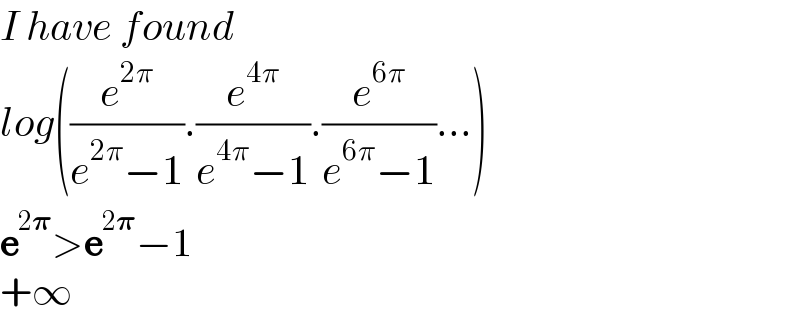
$${I}\:{have}\:{found}\: \\ $$$${log}\left(\frac{{e}^{\mathrm{2}\pi} }{{e}^{\mathrm{2}\pi} −\mathrm{1}}.\frac{{e}^{\mathrm{4}\pi} }{{e}^{\mathrm{4}\pi} −\mathrm{1}}.\frac{{e}^{\mathrm{6}\pi} }{{e}^{\mathrm{6}\pi} −\mathrm{1}}…\right) \\ $$$$\boldsymbol{\mathrm{e}}^{\mathrm{2}\boldsymbol{\pi}} >\boldsymbol{\mathrm{e}}^{\mathrm{2}\boldsymbol{\pi}} −\mathrm{1}\:\:\:\:\: \\ $$$$+\infty \\ $$
Commented by Dwaipayan Shikari last updated on 09/Feb/21

$${But}\:{not}\:{significantly}\:\frac{{e}^{\mathrm{2}\pi} }{{e}^{\mathrm{2}\pi} −\mathrm{1}}=\mathrm{1}.\mathrm{0018}.. \\ $$$$\frac{{e}^{\mathrm{4}\pi} }{{e}^{\mathrm{4}\pi} −\mathrm{1}}<\mathrm{1}.\mathrm{0018} \\ $$$$\frac{{e}^{\mathrm{6}\pi} }{{e}^{\mathrm{6}\pi} −\mathrm{1}}<\frac{{e}^{\mathrm{4}\pi} }{{e}^{\mathrm{4}\pi} −\mathrm{1}}<\mathrm{1}.\mathrm{0018} \\ $$$${So}\:\frac{{e}^{\mathrm{2}\pi} }{{e}^{\mathrm{2}\pi} −\mathrm{1}}.\frac{{e}^{\mathrm{4}\pi} }{{e}^{\mathrm{4}\pi} −\mathrm{1}}.\frac{{e}^{\mathrm{6}\pi} }{{e}^{\mathrm{6}\pi} −\mathrm{1}}…=\left(\mathrm{1}.\mathrm{0018}\right)\left(\mathrm{1}.\mathrm{0018}−\epsilon\right)\left(\mathrm{1}.\mathrm{00018}−\mathrm{2}\epsilon\right)… \\ $$$${So}\:{it}\:{converges}\:\:\:\epsilon=+{ve} \\ $$
Commented by Dwaipayan Shikari last updated on 09/Feb/21
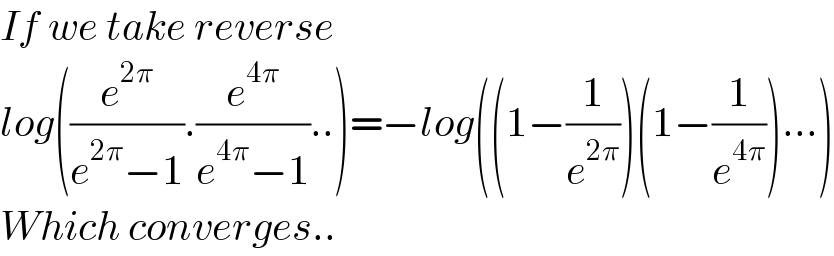
$${If}\:{we}\:{take}\:{reverse} \\ $$$${log}\left(\frac{{e}^{\mathrm{2}\pi} }{{e}^{\mathrm{2}\pi} −\mathrm{1}}.\frac{{e}^{\mathrm{4}\pi} }{{e}^{\mathrm{4}\pi} −\mathrm{1}}..\right)=−{log}\left(\left(\mathrm{1}−\frac{\mathrm{1}}{{e}^{\mathrm{2}\pi} }\right)\left(\mathrm{1}−\frac{\mathrm{1}}{{e}^{\mathrm{4}\pi} }\right)…\right) \\ $$$${Which}\:{converges}.. \\ $$
