Menu Close

n-1-5-12n-2-4-18-2-12n-8-4-18-2-10-4-324-22-4-324-34-4-324-46-4-324-58-4-324-4-4-324-16-4-324-28-4-324-40-4-324-52-4-324-

Tinku Tara 0 Comments
Pin




Question Number 70069 by tw000001 last updated on 01/Oct/19
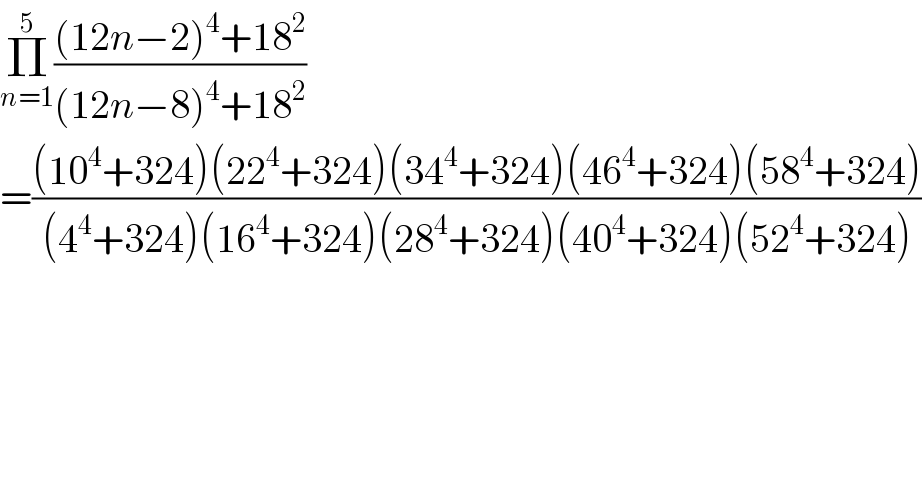
Π_(n=1) ^5 (((12n−2)^4 +18^2 )/((12n−8)^4 +18^2 )) =(((10^4 +324)(22^4 +324)(34^4 +324)(46^4 +324)(58^4 +324))/((4^4 +324)(16^4 +324)(28^4 +324)(40^4 +324)(52^4 +324)))
$$\underset{{n}=\mathrm{1}} {\overset{\mathrm{5}} {\prod}}\frac{\left(\mathrm{12}{n}−\mathrm{2}\right)^{\mathrm{4}} +\mathrm{18}^{\mathrm{2}} }{\left(\mathrm{12}{n}−\mathrm{8}\right)^{\mathrm{4}} +\mathrm{18}^{\mathrm{2}} } \\ $$$$=\frac{\left(\mathrm{10}^{\mathrm{4}} +\mathrm{324}\right)\left(\mathrm{22}^{\mathrm{4}} +\mathrm{324}\right)\left(\mathrm{34}^{\mathrm{4}} +\mathrm{324}\right)\left(\mathrm{46}^{\mathrm{4}} +\mathrm{324}\right)\left(\mathrm{58}^{\mathrm{4}} +\mathrm{324}\right)}{\left(\mathrm{4}^{\mathrm{4}} +\mathrm{324}\right)\left(\mathrm{16}^{\mathrm{4}} +\mathrm{324}\right)\left(\mathrm{28}^{\mathrm{4}} +\mathrm{324}\right)\left(\mathrm{40}^{\mathrm{4}} +\mathrm{324}\right)\left(\mathrm{52}^{\mathrm{4}} +\mathrm{324}\right)} \\ $$
Commented by MJS last updated on 30/Sep/19
just calculate it 373
$$\mathrm{just}\:\mathrm{calculate}\:\mathrm{it} \\ $$$$\mathrm{373} \\ $$
Commented by MJS last updated on 30/Sep/19
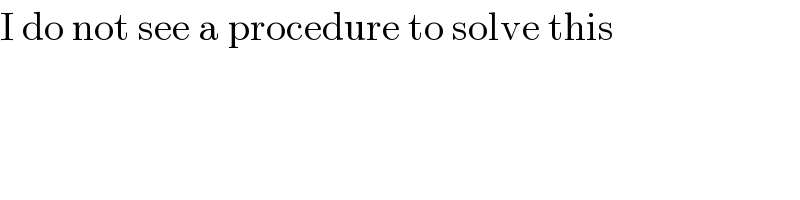
I do not see a procedure to solve this
$$\mathrm{I}\:\mathrm{do}\:\mathrm{not}\:\mathrm{see}\:\mathrm{a}\:\mathrm{procedure}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{this} \\ $$
Answered by tw000001 last updated on 01/Oct/19
Use a^4 +b^4 =(a^2 +2b^2 −2ab)(a^2 +2b^2 +2ab), so it can find out n^4 +324=n^4 +4∙3^4 =[n(n−6)+18][n(n+6)+18]. (((4∙10+18)(10∙16+18)∙∙∙(52∙58+18)(58∙64+18))/((−2∙4+18)(4∙10+18)∙∙∙(52∙58+18))) =((18+58∙64)/(18−2∙4)) =373
$$\mathrm{Use}\:{a}^{\mathrm{4}} +{b}^{\mathrm{4}} =\left({a}^{\mathrm{2}} +\mathrm{2}{b}^{\mathrm{2}} −\mathrm{2}{ab}\right)\left({a}^{\mathrm{2}} +\mathrm{2}{b}^{\mathrm{2}} +\mathrm{2}{ab}\right), \\ $$$$\mathrm{so}\:\mathrm{it}\:\mathrm{can}\:\mathrm{find}\:\mathrm{out}\:{n}^{\mathrm{4}} +\mathrm{324}={n}^{\mathrm{4}} +\mathrm{4}\centerdot\mathrm{3}^{\mathrm{4}} =\left[{n}\left({n}−\mathrm{6}\right)+\mathrm{18}\right]\left[{n}\left({n}+\mathrm{6}\right)+\mathrm{18}\right]. \\ $$$$\frac{\left(\mathrm{4}\centerdot\mathrm{10}+\mathrm{18}\right)\left(\mathrm{10}\centerdot\mathrm{16}+\mathrm{18}\right)\centerdot\centerdot\centerdot\left(\mathrm{52}\centerdot\mathrm{58}+\mathrm{18}\right)\left(\mathrm{58}\centerdot\mathrm{64}+\mathrm{18}\right)}{\left(−\mathrm{2}\centerdot\mathrm{4}+\mathrm{18}\right)\left(\mathrm{4}\centerdot\mathrm{10}+\mathrm{18}\right)\centerdot\centerdot\centerdot\left(\mathrm{52}\centerdot\mathrm{58}+\mathrm{18}\right)} \\ $$$$=\frac{\mathrm{18}+\mathrm{58}\centerdot\mathrm{64}}{\mathrm{18}−\mathrm{2}\centerdot\mathrm{4}} \\ $$$$=\mathrm{373} \\ $$
Commented by MJS last updated on 01/Oct/19
please show in easy steps how to transform (((12n−2)^4 +18^2 )/((12n−8)^4 +18^2 )) into your solution, I don′t think this is easy to see
$$\mathrm{please}\:\mathrm{show}\:\mathrm{in}\:\mathrm{easy}\:\mathrm{steps}\:\mathrm{how}\:\mathrm{to}\:\mathrm{transform} \\ $$$$\frac{\left(\mathrm{12}{n}−\mathrm{2}\right)^{\mathrm{4}} +\mathrm{18}^{\mathrm{2}} }{\left(\mathrm{12}{n}−\mathrm{8}\right)^{\mathrm{4}} +\mathrm{18}^{\mathrm{2}} }\:\mathrm{into}\:\mathrm{your}\:\mathrm{solution},\:\mathrm{I}\:\mathrm{don}'\mathrm{t} \\ $$$$\mathrm{think}\:\mathrm{this}\:\mathrm{is}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{see} \\ $$
Commented by mind is power last updated on 01/Oct/19
x^4 +4y^4 =(x^2 +2y^2 )^2 −4x^2 y^2 =(x^2 +2y^2 −2xy)(x^2 +2y^2 +2xy) for x=12n−2 and y=3 ⇒(12n−2)^4 +4.3^4 =((12n−2)^2 +2.9−2.3(12n−2))((12n−2)^2 +2.9+6(12n−2)) =(144n^2 −120n+34)(144n^2 +24n+10) (12n−8)^4 +4.3^4 =((12n−8)^2 +2.3^2 −2.3(12n−8))((12n−8)^2 +18+6(12n−8)) =(144n^2 +130−264n)(144n^2 −120n+34) Π(((12n−2)^4 +18^2 )/((12n−8)^4 +18^2 ))=Π(((144n^2 +24n+10)(144n^2 −120n+34))/((144n^2 −120n+34)(144n^2 −264n+130))) =Π_(k=1) ^m ((144n^2 +24n+10)/(144n^2 −264n+130))=((Π_(k=1) ^m (144n^2 +24n+10))/((144−264+130)Π_(k=1) ^(m−1) (144(n+1)^2 −264(n+1)+130))) =((Π_(k=1) ^m (144n^2 +24n+10))/(10Π_(k=1) ^m (144n^2 +288n+144−264n−264+130)))=((Π_(k=1) ^m (144n^2 +24n+10))/(10.Π_(k=1) ^(m−1) (144n^2 +24n+10))) =((144m^2 +24m+10)/(10)) Hop this help you sir MJS
$${x}^{\mathrm{4}} +\mathrm{4}{y}^{\mathrm{4}} =\left({x}^{\mathrm{2}} +\mathrm{2}{y}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{4}{x}^{\mathrm{2}} {y}^{\mathrm{2}} =\left({x}^{\mathrm{2}} +\mathrm{2}{y}^{\mathrm{2}} −\mathrm{2}{xy}\right)\left({x}^{\mathrm{2}} +\mathrm{2}{y}^{\mathrm{2}} +\mathrm{2}{xy}\right) \\ $$$${for}\:{x}=\mathrm{12}{n}−\mathrm{2}\:{and}\:{y}=\mathrm{3} \\ $$$$\Rightarrow\left(\mathrm{12}{n}−\mathrm{2}\right)^{\mathrm{4}} +\mathrm{4}.\mathrm{3}^{\mathrm{4}} =\left(\left(\mathrm{12}{n}−\mathrm{2}\right)^{\mathrm{2}} +\mathrm{2}.\mathrm{9}−\mathrm{2}.\mathrm{3}\left(\mathrm{12}{n}−\mathrm{2}\right)\right)\left(\left(\mathrm{12}{n}−\mathrm{2}\right)^{\mathrm{2}} +\mathrm{2}.\mathrm{9}+\mathrm{6}\left(\mathrm{12}{n}−\mathrm{2}\right)\right) \\ $$$$=\left(\mathrm{144}{n}^{\mathrm{2}} −\mathrm{120}{n}+\mathrm{34}\right)\left(\mathrm{144}{n}^{\mathrm{2}} +\mathrm{24}{n}+\mathrm{10}\right) \\ $$$$\left(\mathrm{12}{n}−\mathrm{8}\right)^{\mathrm{4}} +\mathrm{4}.\mathrm{3}^{\mathrm{4}} =\left(\left(\mathrm{12}{n}−\mathrm{8}\right)^{\mathrm{2}} +\mathrm{2}.\mathrm{3}^{\mathrm{2}} −\mathrm{2}.\mathrm{3}\left(\mathrm{12}{n}−\mathrm{8}\right)\right)\left(\left(\mathrm{12}{n}−\mathrm{8}\right)^{\mathrm{2}} +\mathrm{18}+\mathrm{6}\left(\mathrm{12}{n}−\mathrm{8}\right)\right) \\ $$$$=\left(\mathrm{144}{n}^{\mathrm{2}} +\mathrm{130}−\mathrm{264}{n}\right)\left(\mathrm{144}{n}^{\mathrm{2}} −\mathrm{120}{n}+\mathrm{34}\right) \\ $$$$\Pi\frac{\left(\mathrm{12}{n}−\mathrm{2}\right)^{\mathrm{4}} +\mathrm{18}^{\mathrm{2}} }{\left(\mathrm{12}{n}−\mathrm{8}\right)^{\mathrm{4}} +\mathrm{18}^{\mathrm{2}} }=\Pi\frac{\left(\mathrm{144}{n}^{\mathrm{2}} +\mathrm{24}{n}+\mathrm{10}\right)\left(\mathrm{144}{n}^{\mathrm{2}} −\mathrm{120}{n}+\mathrm{34}\right)}{\left(\mathrm{144}{n}^{\mathrm{2}} −\mathrm{120}{n}+\mathrm{34}\right)\left(\mathrm{144}{n}^{\mathrm{2}} −\mathrm{264}{n}+\mathrm{130}\right)} \\ $$$$=\underset{{k}=\mathrm{1}} {\overset{{m}} {\prod}}\frac{\mathrm{144}{n}^{\mathrm{2}} +\mathrm{24}{n}+\mathrm{10}}{\mathrm{144}{n}^{\mathrm{2}} −\mathrm{264}{n}+\mathrm{130}}=\frac{\underset{{k}=\mathrm{1}} {\overset{{m}} {\prod}}\left(\mathrm{144}{n}^{\mathrm{2}} +\mathrm{24}{n}+\mathrm{10}\right)}{\left(\mathrm{144}−\mathrm{264}+\mathrm{130}\right)\underset{{k}=\mathrm{1}} {\overset{{m}−\mathrm{1}} {\prod}}\left(\mathrm{144}\left({n}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{264}\left({n}+\mathrm{1}\right)+\mathrm{130}\right)} \\ $$$$=\frac{\underset{{k}=\mathrm{1}} {\overset{{m}} {\prod}}\left(\mathrm{144}{n}^{\mathrm{2}} +\mathrm{24}{n}+\mathrm{10}\right)}{\mathrm{10}\underset{{k}=\mathrm{1}} {\overset{{m}} {\prod}}\left(\mathrm{144}{n}^{\mathrm{2}} +\mathrm{288}{n}+\mathrm{144}−\mathrm{264}{n}−\mathrm{264}+\mathrm{130}\right)}=\frac{\underset{{k}=\mathrm{1}} {\overset{{m}} {\prod}}\left(\mathrm{144}{n}^{\mathrm{2}} +\mathrm{24}{n}+\mathrm{10}\right)}{\mathrm{10}.\underset{{k}=\mathrm{1}} {\overset{{m}−\mathrm{1}} {\prod}}\left(\mathrm{144}{n}^{\mathrm{2}} +\mathrm{24}{n}+\mathrm{10}\right)} \\ $$$$=\frac{\mathrm{144}{m}^{\mathrm{2}} +\mathrm{24}{m}+\mathrm{10}}{\mathrm{10}} \\ $$$${Hop}\:{this}\:{help}\:{you}\:{sir}\:{MJS} \\ $$$$ \\ $$
Commented by MJS last updated on 01/Oct/19
thank you
$$\mathrm{thank}\:\mathrm{you} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *